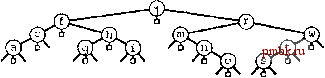РИСУНОК 10.13. ПРИМЕР УЗЛОВ ДЕРЕВА ТРЕХПУТЕВОЙ ПОРАЗРЯДНОЙ БЫСТРОЙ СОРТИРОВКИ.

Трехпутевая поразрядная быстрая сортировка подходит к решению проблемы пустых корзин, характерной для поразрядной сортировки MSD, с применением трехпутевого разбиения, чтобы устранить значение одного байта и (в рекурсивном режиме) работать с другими. Это действие соответствует замене каждого узла на пути вдоль средних связей по дереву, которое описывает рекурсивную структуру вызовов поразрядной сортировки MSD (см. рис. 10.9) на троичное дерево, в котором каждой непустой корзине соответствует внутренний узел. Для полных узлов (слева) такое изменение требует затрат времени и не влечет за собой заметной экономии пространства памяти, в то время как в случае пустых узлов (справа), затраты времени минимальны, а экономия памяти значительная.

Мы можем разработать гибридный метод, пригодный для многих практических приложений, обладающий превосходными характеристиками, применяя стандартную поразрядную сортировку MSD для упорядочения крупных файлов, чтобы воспользоваться преимуществами многопутевого разбиения, и трехпутевую поразрядную сортировку с небольшим значением основания системы счисления для небольших файлов, чтобы избежать отрицательных эффектов, обусловленных наличием большого числа пустых корзин.

Трехпутевая быстрая сортировка успешно применяется и в тех случаях, когда сортируемыми ключами являются векторы (как в математическом смысле, так и в смысле стандартной библиотеки шаблонов С++. Другими словами, если ключи составлены из независимых компонентов (каждый компонент сам по себе независимый ключ), мы имеем возможность переупорядочить записи таким образом, что они будут располагаться в порядке следования первых компонентов ключей и в порядке следования вторых компонентов ключей в тех случаях, когда равны их первые компоненты и т.д. Мы можем рассматривать сортировку векторов как обобщенный вид поразрядной сортировки, где R может быть произвольно большим. После выполнения настройки программы 10.3 на это приложение, мы будем называть ее многомерной быстрой сортировкой (тиШкеу quicksort).

Упражнения

10.25. Для d > 4 предположим, что ключи состоят из d байтов, при этом заключительные 4 байта принимают случайные значения, а все остальные равны 0. Дайте оценку количеству просмотренных байтов при сортировке посредством методов трехпутевой поразрядной быстрой сортировки (Профамма 10.3) и стандартной быстрой сортировки (Профамма 7.1) файла размером Лдля больших Л, и вычислите для обоих случаев отношение значений времени выполнения сортировки.

10.26. Эмпирически определите размер байта, для которого время выполнения трехпутевой сортировки 64-разрядных ключей минимально, при N= 10 IC*, 10 и 10

10.27. Разработать реализацию трехпутевой поразрядной сортировки для связных списков.

10.28. Разработать реализацию многопутевой поразрядной сортировки для случая, когда ключи представлены в виде векторов из / чисел с плавающей точкой, используя проверку чисел с плавающей точкой на равенство, описанную в упражнении 4.6.

10.29. Используя генератор ключей, описанный в упражнении 10.19, выполнить трехпутевую поразрядную быструю сортировку для = 10

10 *, 10 и 10. Сравнить ее производительность с аналогичным показателем для поразрядной сортировки MSD.

10.30. Используя генератор ключей, описанный в упражнении 10.21, выполнить трехпутевую поразрядную быструю сортировку для 7V = 10, 10 *, 10 и 10. Сравнить ее производительность с аналогичным показателем для поразрядной сортировки MSD.

10.31. Используя генератор ключей, описанный в упражнении 10.23, выполнить трехпутевую поразрядную быструю сортировку для = 10, 10 , 10 и 10 Сравнить ее производительность с аналогичным показателем для поразрядной сортировки MSD.

10.5. Поразрядная сортировка LSD

Метод, альтернативный поразрядной сортировке, предусматривает просмотр байтов в направлении справа налево. На рис. 10.14 показано, как задача сортировки трехбуквенных слов может быть рещена за три прохода по файлу. Мы сначала сортируем файл по последней букве (используя для этой цели метод подсчета индексных ключей), затем по средней букве, и только потом - по первой букве.

На первых порах не так то просто поверить, что этот метод работает; и в самом деле, он вообще не работает, если используемый метод сортировки неустойчив (см. определение 6.1). После того, как установлена важность свойства устойчивости, нетрудно дать формулировку доказательства того, что поразрядная сортировка LSD работает: мы знаем, что после упорядочения ключей по / замыкающим байтам (при сохранении устойчивости) любые два ключа в файле появляются в нужном порядке (в соответствии с просмотренными на текущий момент разрядами) либо благодаря тому, что первые из / замыкающих байтов отличны друг от друга, в подобном случае сортировка по этому байту расставила их в соответствующем порядке, или если первые из / замыкающих байтов совпадают, они уже упорядочены нужным образом в силу свойства устойчивости. Можно дать этому другую формулировку: если w - i еще не просмотренных байтов какой-

ПОРАЗРЯДНОЙ СОРТИРОВКИ LSD

Трехбуквенные слова упорядочиваются за три прохода (oieea направо) методом поразрядной сортировки LSD

либо пары ключей идентичны, то любое различие между этими ключами определяется / байтами, которые уже просмотрены, и если эти ключи должным образом упорядочены, то они сохраняют этот порядок в силу свойства устойчивости. С другой стороны, если W - i еще не просмотренных байтов различны, то те / байтов, которые уже просмотрены, не играют никакой роли, так что следующий проход должным образом упорядочит эту пару, учитывая различия в более значащих байтах.

Требование устойчивости означает, например, что метод разделения, использованный в двоичной быстрой сортировке, не может быть использован в двоичной версии рассматриваемого метода сортировки справа налево. С другой стороны, метод сортировки с подсчетом индексных ключей является устойчивым методом сортировки, что сразу же приводит нас к классическому и эффективному алгоритму. Программа 10.4 представляет собой реализацию этого метода. По-видимому, понадобится вспомогательный массив для целей распределения - методы, которые используются в упражнениях 10.17 и 10.18, выполняющие распределение без использования дополнительной памяти, жертвуют устойчивостью в пользу отказа от дополнительного массива.

Метод поразрядной сортировки использовался в старых машинах для сортировки перфокарт для вычислительных машин. Такие, машины обладали способностью распределения колоды карт по 10 корзинам в соответствии видом отверстий, пробитых в специальных столбцах. Если в некотором наборе столбцов пробиты определенные числа, оператор может сортировать перфокарты, пропуская их через машину по крайней правой цифре, затем собрав и упорядочив колоды перфокарт, полученные на выходе, снова пропустить их через машину, на сей раз по цифре, следующей за крайней правой, и т.д. Физическая сортировка перфокарт представляет собой устойчивый процесс, который можно смоделировать сортировкой методом подсчета индексных ключей. Эта версия поразрядной сортировки LSD не только широко использовалась в коммерческих приложениях в пятидесятых и шестидесятых годах прошлого столетия, этим методом пользовались многие осторожные программисты, которые пробивали некоторые последовательности чисел в нескольких концевых колонках колоды перфокарт, на которых набита программа, чтобы можно было восстановить порядок следования перфокарт в колоде механическим способом, если колода случайно рассыплется.

Программа 10.4. Метод поразрядной сортировки LSD

Данная программа реализует сортировку байтов в словах методом подсчета индексных ключей, продвигаясь слева направо. Реализация сортировки методом подсчета индексных ключей должна быть устойчивой. Если R равна 2 (благодаря чему bytesword и bitwords идентичны), данная программа является прямой поразрядной сортировкой - с проходом справа налево, с поразрядным просмотром (см. рис. 10.15).

template <class Item> void radixLSD(Item a[] , int 1, int r) { static Item aux[maxN];

for (int d = bytesword-l; d >= 0; d-) {

int i, j, count[R+1];

for (j = 0; j < R; j++) count [j] = 0;