Сравнивая трехпутевую поразрядную быструю сортировку со стандартной поразрядной сортировкой MSD мы можем отметить, что она разбивает файл всего лишь на три части, так что она не использует всех преимуществ быстрого многопутевого разбиения, особенно на ранних стадиях сортировки. С другой стороны, на поздних стадиях поразрядной сортировки MSD появляется множество пустых корзин, но в то же время поразрядная быстрая сортировка хорошо приспособлена для случаев дублированных ключей, ключей, принимающих значения в узких диапазонах, файлов небольших размеров и многих других случаев, в условиях которых поразрядная сортировка MSD выполняется медленно. Особо важное значение приобретает то обстоятельство, что подобного рода разбиение хорошо подходит для случаев проявления различного рода закономерностей в разных частях ключа. Более того, для нее не нужны никакие вспомогательные файлы. В противовес всем этим достоинствам можно поставить тот факт, что требуются дополнительные операции обмена, чтобы реализовать многопутевое разбиение с помощью трехпутевого разбиения, когда число подфайлов велико.

На рис. 10.11 приводится пример применения этого метода для сортировки совокупности трехбуквенных слов, представленных на рис. 10.7. Рисунок 10.12 отражает структуру рекурсивных вызовов. Каждый узел соответствует в точности трем рекурсивным вызовам: по ключам с меньшим значением первого байта (левый потомок), по ключам с тем же значением первого байта (средний потомок) и по ключам с большим значением первого байта (правый потомок).

Когда сортируемые ключи соответствуют абстракции из раздела 10.2, стандартную быструю сортировку (а также все другие методы сортировки, рассмотренные в главах 6-9) можно рассматривать как поразрядную сортировку MSD, поскольку функция сравнения осуществляет доступ сначала к наиболее значащей части ключа (см. упражнение 10.3). Например, если в качестве ключей выступают строки, функция сравнения должна осуществлять доступ только к старшим байтам, если они попарно различаются, и к двум байтам, если первые байты совпадают, а вторые байты различны, и т.д. Таким образом, стандартный алгоритм автоматически затрачивает некоторую часть выигрыша в производительности, в погоне за которой мы используем поразрядную сортировку MSD (см. раздел 7.7). Существенное различие заключается в том, что стандартный алгоритм не может предпринять никаких действий, когда старшие байты равны.

iK>v асе f 0(г fox ЫХ tip dug diig

ilk ilk cab

dim dim tiTi tag ago ago jot and aad

sob fee egg йоЪ cue cue sky caw caw

ago ago Ьег ace and and

ace bet

cab caw cue

6 dug diffi

hut kut fee aoe ace for bet bet few

men cab ilk

eg egg Si-S few few hut

jay jay jaL ои1 jot jay

joy joy joy rap j-am jet

gig ovl 07l Ш&

wee wee now was was nob cab шеи men

ovl acb aov

wad wad rap

caw sky sky cue nob was

fee sob s b tap tap tap ago tag tag

tar tax tar

dug tip tip and now wee jam rap wad

sky sky tip sob

sob tip tax

tap tap tap

tag tag tag

tax tax tip

РИСУНОК 10.11.

ТРЕХПУТЕВАЯ

ПОРАЗРЯДНАЯ

БЫСТРАЯ

СОРТИРОВКА

Мы делим файл на три

части: слова,

начинающиеся с букв

от а до i, слова,

начинающиеся с буквы

j, и слова,

начинающиеся с букв от к до Z. Затем мы выполняем сортировку в рекурсивном режиме.

10 программой FmePnnt - Купить W

Действительно, программу 10.3 можно рассматривать как способ метода быстрой сортировки запоминать все, что ему стало известно о старших цифрах элементов после их использования в процедуре разделения файла на несколько частей. В малых файлах, для которых большая часть операций сравнения была выполнена в процессе сортировки, существует большая вероятность того, что многие старшие байты совпадают. Стандартный алгоритм обязан просмотреть все эти байты в рамках каждой операции сравнения, в то время как трехпутевой алгоритм не делает этого.

Программа 10.3. Трехпутевая поразрядная быстрая сортировка

Программный код поразрядной сортировки MSD фактически мало чем отличается от программного кода быстрой сортировки с трехпутевым разбиением (программа 9.5), отличия состоят в следующем: (/) ссылки на ключи становятся ссылками на конкретные байты ключей, ( ) текущий байт добавляется как параметр к рекурсивной служебной программе и ( /) рекурсивные вызовы для среднего подфайла перемещаются к следующему байту. Мы избегаем выполнять перемещения за пределы концов строк путем проверки, равно ли разделяющее значение О, перед рекурсивными обращениями, которые обеспечивают переход к следующим байтам. Когда разделяющим значением является О, левый подфайл пуст, средний подфайл соответствует ключам, которые, по определению программы, равны этому значению, а правый подфайл соответствует более длинным строкам, которые требуют дальнейшей обработки.

#define ch(A) digit(А, d) template <class Item>

void cjuicksortXdtem a[] , int 1, int r, int d)

int i, j, k, p, q; int v;

if (r-1 <= M) ( insertion(a, 1, r) ; return; } v = ch(a[r]); i = 1-1; j = r; p = 1-1; q = r; while (i < j) {

while (ch(a[++i]) < v) ;

while (V < ch(a[-j])) if (j == 1) break; if (i > j) break; exch(a[i], a[j]);

if (ch(a[i])=v) { Р++; exch(a[p], a[i]); } if (v=ch(a[j])) ( q-; exch(a[j] , a[q]); }

if (p == q) { if (V != \0 ) quicksortX (a, 1, r, d+1); return; } if (ch(a[i]) < V) i++;

for (k = 1; к <= p; k++, j -) exch(a[k] , a[j]);

for (k = r; к >= q; k-, i++) exch(a[k] , a[i]);

c[uicksortX(a, 1, j, d) ;

if ((i = r) && (ch(a[i]) == V)) i++;

if (v != \0 ) quicksortX(a, j+1, i-1, d+1);

c[uicksortX(a, i, r, d) ;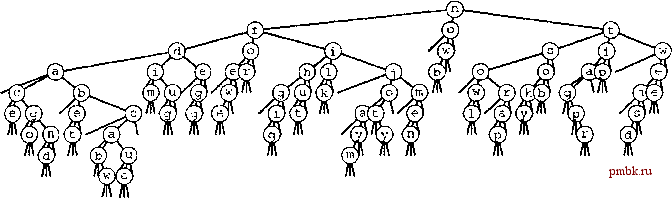

>

РИСУНОК 10.12. РЕКУРСИВНАЯ СТРУКТУРА ТРЕХПУТЕВОЙ ПОРАЗРЯДНОЙ БЫСТРОЙ СОРТИРОВКИ

Представленная на диаграмме комбинация двоичного и троичного деревьев соответствует подстановке 26-путевых узлов в двоичное дерево, изображенное на рис. 10.10, троичных деревьев поиска, как показано на рис. 10.13. Любой путь от корня на нижний уровень дерева, который оканчивается средней связью, определяет ключ файла, задаваемый символами, охваченными средними связями на этом пути. В диаграмме, показанной на рис. 10.10, имеется 1035 пустых связей, которые не отображены на ней, что касается рассматриваемой диаграммы, то все 155 пустых связей, которыми обладает это дерево, на диаграмме показаны. Каждая пустая связь соответствует пустой корзине, так что это различие показывает, как трехпутевой разбиение может существенно сократить число пустых корзин, которые появляются во время поразрядной сортировки MSD.

Рассмотрим случай, когда ключи имеют большую длину (для простоты предположим, что длина ключей фиксирована) и в то же время по большей части старшие байты одинаковы. В подобного рода ситуациях время выполнения обычной быстрой сортировки пропорционально длине слова, помноженной на 2N\nN, тогда как время выполнения ее поразрядной версии пропорционально Л, умноженному на длину слова (чтобы обнаружить все равные между собой старшие байты) плюс 2N \nN (затрачивается на сортировку более коротких ключей). Иначе говоря, этот метод работает в 1пЛ раз быстрее, чем обычная быстрая сортировка, если принимать во внимание только стоимость операций сравнения. Для ключей, используемых в сортировочных приложениях на практике, характеристики, подобные полученным в условиях рассмотренного выше искусственного примера, не являются чем-то необычным (см. упражнение 10.25).

Другим интересным свойством трехпутевой поразрядной быстрой сортировки является то, что ее характеристики напрямую не зависят от значения основания системы счисления. Для других методов сортировки, использующих основание системы счисления, нужно заводить и поддерживать вспомогательный массив, индексированный по значению основания системы счисления. Также следует позаботиться о том, чтобы размер этого массива ненамного превосходил размер самого файла. Для этого метода нет такой таблицы. Если в качестве основания брать исключительно большое значение (больше длины слова), то рассматриваемый метод превращается в обычную быструю сортировку, а если в качестве основания взять число 2, то он вырождается в обычную двоичную быструю сортировку, и только промежуточные значения основания системы счисления позволяют эффективно преодолевать равные промежутки между фрагментами ключей.