процедуру двоичной быстрой сортировки, которая модифицирована таким образом, что игнорирует эти разряды. Сравнить время выполнения вашей программы со временем выполнения стандартной реализации для N = 10 10*, 10 и 10, когда в качестве входных данных используется 32-разрядные слова следующего формата: крайние правые 16 битов - это равномерно распределенные случайные значения, а все крайние левые 16 битов суть О за исключением ситуаций, когда в позициях / проставляется 1, если имеется / единиц в правой половине.

10.13. Внести изменения в двоичную быструю сортировку с целью непосредственного обнаружения ситуаций, когда все ключи равны. Сравните время выполнения вашей программы с аналогичным показателем для стандартной реализации при Л = 10, 10*, 10 и 10 для случая, когда входными данными служат данные, описанные в упражнении 10.12.

10.3. Поразрядная сортировка MSD

Использование всего лишь 1 разряда при поразрядной быстрой сортировке заставляет нас рассматривать ключи как числа в двоичной системе счисления и рассматривать сначала наиболее значащие числа. Обобщая предположим, что мы хотим отсортировать числа, представленные в системе счисления по основанию R, рассматривая в первую очередь наиболее значащие байты. Чтобы сделать это, необходимо разделить массив по крайней мере на R, а не на 2, различных частей. По традиции будем называть эти разделы корзинами или ведрами и будем представлять себе рассматриваемый алгоритм как группу из R корзин, по одной на каждое возможное значение первой цифры, как показано на следующей диаграмме: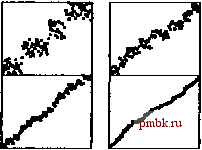

РИСУНОК 10.6. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОРАЗРЯДНОЙ СОРТИРОВКИ MSD

Всего лишь одна стадия поразрядной сортировки MSD почти полностью решает задачу упорядочения, как показывает рассматриваемый пример файла произвольной организации, состоящий из 8-разрядных целых чисел. Первая стадия поразрядной сортировки MSD по двум старшим разрядам (слева) делит исходный файл на четыре подфайла. На следующей стадии каждый такой подфайл делится на четыре подфайла. Поразрядная сортировка MSD по трем старшим разрядам (справа) делит файл на восемь подфайлов за один проход, на котором также выполняются распределение и подсчет. На следующем уровне каждый из этих подфайлов снова разбивается на восемь частей, при этом в каждой такой части содержатся всего лишь несколько элементов.

bin[0]

bin[l]

bin[2]

bin[М-1]

Мы выполняем проход по всем ключам, распределяя их по корзинам, затем выполняем сортировку содержимого корзины по ключам с байтами, которые меньше исходных на 1.

На рис. 10.6 показан пример поразрядной сортировки MSD на произвольных перестановках целых чисел. В отличие от двоичной быстрой сортировки этот алгоритм может привести файл в относительный порядок достаточно быстро, даже после первого разделения, если значение основания системы счисления достаточно велико.

Как уже говорилось в разделе 10.2, одна из наиболее привлекательных особенностей поразрядной сортировки обусловлена ее интуитивным и прямолинейным характером, позволяющим ее адаптироваться к сортирующим приложениям, в условиях которых ключами являются символьные строки. Это ее свойство особенно ярко проявляется в С++ и других средах программирования, в которых обеспечена прямая поддержка обработки строк, В условиях поразрядной сортировки мы просто используем основание системы счисления, соответствующее размеру байта. Чтобы извлечь цифру, мы загружаем байт, чтобы переместиться к следующей цифре, мы увеличиваем на единицу указатель строки. Сейчас мы рассматриваем строки фиксированной длины, а немного погодя мы убедимся в том, что с ключами в виде строк переменной длины легко работать, используя те же базовые механизмы.

На рис. 10.7 показан пример поразрядной сортировки MSD трехбуквенных слов. Для простоты изложения в условиях этого примера за основание системы счисления принимается значение 26, хотя для большей части приложений мы выбираем с этой целью большее значение основания, в зависимости от того, как кодируются символы. Прежде всего, слова переупорядочиваются таким образом, что те из них, которые начинаются с символа а, идут раньше слов, начинающихся с буквы Ь, и т.д. Затем слова, начинающиеся с буквы а, подвергаются рекурсивной сортировке, далее производится сортировка слов, начинающихся с буквы Ь, и т.д. Как показывает пример, большая часть работы, связанной с сортировкой, приходится на разделения по первой букве, полученные после первого разделения подфайлы имеют небольшие размеры.

Как мы уже убедились на примере быстрой сортировки в главах 7 и разделе 10.2, а также при ознакомлении с сортировкой слиянием в главе 8, можно повысить эффективность большинства рекурсивных программ за счет использования простых алгоритмов для сортировки небольших по размерам файлов. Вопрос использования других методов для сортировки файлов

now асе асе асе

for ago ago ago

tip and and cmd ilk bet bet bet dim cab cab cab

tag caw caw caw

jot cue cue cue sob dim dim dim

nob dug dug dug sky egg egg egg hut for few fee

ace fee fee few

bet few for for men gig gig gig egg hut hut hut

few ilk ilk ilk

jay jam jay jam

owl jay jam jay

joy jot jot j

rap joy joy joy gig men men men wee now now nob

was nob nob now

cab owl owl owl

wad rap rap rap

caw sob sky sky

cue sky sob sob fee tip tag tag

tap tag tap tap

ago tap tax tar

tar tax tip tip jam wee wad wad

dug was was was

and wad wee wee

рисунок 10.7. пример

поразрядной сортировки msd

Мы распределяем множество слов по 26 корзинам соответственно первой букве. Затем мы сортируем каждую корзину, применяя тот же метод, начиная со второй буквы.

небольших размеров (корзины, содержащие небольшое число элементов) имеет большое значение для поразрядной сортировки, ибо их так много! Более того, мы можем настроить алгоритм соответствующим образом путем выбора значения R, поскольку существует простая зависимость; если R принимает чрезмерно большое значение, то большая часть стоимости сортировки приходится на инициализацию и проверку корзин, если наоборот, R недостаточно велико, то метод не использует своих потенциальных выгод, что достигается, если разделить исходный файл на максимально возможное число фрагментов. Мы вернемся к исследованию этих проблем в конце разделе 10.6.

Чтобы реализовать поразрядную сортировку MSD, необходимо обобщить методы разделения массивов, которые мы рассматривали при изучении реализаций быстрой сортировки в разделе 10.7. Эти методы, в основу которых положено перемещение указателей с противоположных концов массива навстречу друг другу, так что они встречаются где-то посередине, работают хорошо при необходимости получения двух или трех разделов, но не допускают немедленного обобщения. К счастью, метод подсчета индексных ключей, который рассматривался в главе 6 для целей сортировки файлов с ключами, принимающих значения в узком диапазоне, в рассматриваемом случае подходит как нельзя лучше. При этом используются таблицы значений и вспомогательные массивы, на первом проходе массива подсчитывается количество повторений каждой цифры старшего разряда. Эти значения показывают, где окажутся точки разделения. Затем, на втором проходе массива мы используем эти значения для перемещения элементов в соответствующие позиции вспомогательного массива.

Программа 10.2 реализует этот процесс. Ее рекурсивная структура обобщает структуру быстрой сортировки, так что мы снова оказываемся перед необходимостью решать проблемы, которые рассматривались в разделе 7.3. Должны ли мы сохранять наибольший из подфайлов во избежание излишней глубины рекурсии? Скорее всего, нет, поскольку глубина рекурсии ограничивается длиной ключа. Должны ли мы применять для сортировки подфайлов небольшого размера- простые методы, такие как, например, сортировка простыми вставками? Конечно, поскольку существует огромное число таких методов.

Чтобы выполнить разбиение, программа 10.2 использует вспомогательный массив, размер которого равен размеру файла, подлежащего сортировке. В качестве альтернативы мы можем воспользоваться обменным методом подсчета индексных ключей (см. упражнения 10.17 и 10.18). Мы должны уделить большое внимание использованию пространства памяти, поскольку рекурсивные обращения могут привести к чрезмерному расходу памяти для локальных переменных. В программе 10.2 временный буфер для размещения ключей (aux) может быть глобальным, но массив, в котором хранятся число и местоположение позиций точек разделения (count) должны быть локальными.

Дополнительное пространство памяти для вспомогательного массива не представляют собой сколь-нибудь серьезной проблемы в условиях многочисленных приложений поразрядной сортировки применительно к длинным ключам или записям, поскольку для этих типов данных успешно применяется сортировка по указателю. Следовательно, дополнительное пространство памяти отводится для переупорядоче-