количества битов в машинном слове, от представления целых чисел и отрицательных чисел в той или иной машине. Для однобуквенных 5-разрядных ключей на рис. 10.2 и 10.3 отправной точкой на 32-разрядной машине должен быть бит 27.

Этот пример обращает внимание на потенциальную проблему, возникающую при использовании двоичной быстрой сортировки в реальных ситуациях: вырожденные разделения (когда все ключи имеют одно и то же значение разряда, по которому производится разделение) могут встречаться довольно часто. Такая ситуация при сортировке малых чисел (старшие разряды принимают значение 0), таких как в рассматриваемых нами примерах, не является чем-то необычным. Эта же проблема возникает при использовании ключей, состоящих из символов: например, предположим, что мы строим 32-разрядные ключи из четырех символов, каждый из которых представлен в стандартном 8-разрядном коде, объединяя их в единое целое. Тогда появление вырожденных разделений возможно в начальной позиции каждого символа, поскольку, например, все буквы нижнего регистра начинаются с одних и тех же битов для большинства кодов символов. Эта проблема является типовой по своим последствиям, с которыми приходится сталкиваться при сортировке кодированных данных, подобные проблемы возникают и в других видах поразрядной сортировки.

S О R Т I

N G Е X А М Р L Е

? о 1

0 111*

1 с о 1 :i 101:0

0 10 0 1

о 1 1 i)

0 с 1 1 t <; о 1 : 1

1 1 f; о (-о с о о 1

0 110 1

1 с f> о г.

А Е О L М !

N G Е А X Т Р R S

о о а 1

0 1 о 1 ) : 1 о .-.

10 0 1

1 1 ; о

0 11 1: Г< 1 о 1

0 0 0 1: ; ;) о i

0-1 о о о о

0 0 10, 0 0 11

РИСУНОК 10.3. ПРИМЕР ДВОИЧНОЙ БЫСТРОЙ СОРТИРОВКИ (ПОКАЗАНЫ ЗНАЧЕНИЯ РАЗРЯДОВ КЛЮЧЕЙ)

Мы построили эту диаграмму на основании рис 10.2 путем перевода значений ключей в их двоичные коды и сжатия таблицы, что позволяет показать, как производятся сортировки независимых подфайлов, как если бы они выполнялись параллельно, при этом столбцы и ряды меняются местами. На первой стадии файл разбивается на подфайл, все ключи которого начинаются с О, и на подфайл, все ключи которого начинаются с 1. Затем первый подфайл разбивается на подфайл, все ключи которого начинаются с 00 и на подфайл, все ключи которого начинаются с 01; независимо от этого процесса в некоторый другой момент времени второй подфайл разбивается на подфайл, все ключи которого начинаются с 10 и на подфайл, все ключи которого начинаются с 11. Этот процесс прекратится только тогда, когда все разряды будут исчерпаны (для дублированных ключей в рассматриваемом примере) или когда размер подфайла становится равным 1.

После того как выяснится, что один из ключей отличается от всех остальных значением левого разряда, никакие другие разряды больше не анализируются. Это свойство в одних ситуациях выступает как достоинство, в других - как недостаток. Когда ключи представляют собой случайные совокупности битов, анализу подвергаются только Ig N битов, что намного меньше числа битов в ключах. Этот факт рассматривается в разделе 10.6, а также в упражнении 10.5 и рис. 10.1. Например, сортировка файла из 1000 записей с произвольно организованными ключами может потребовать анализа всего лишь 10 или 11 битов каждого ключа (даже если такими ключами являются, скажем, 64-разрядные ключи).

С другой стороны, все биты одинаковых ключей также проверяются. Поразрядная сортировка не способна работать хорошо на файлах, которые содержат большое число дублированных ключей достаточно большой длины. Двоичная быстрая сортировка и стандартные методы работают достаточно быстро, если сортируемые ключи представляют собой наборы битов случайной природы (различие между ними определяются главным образом разницей стоимости операций извлечения битов и сравнения), но в то же время стандартный алгоритм быстрой сортировки легче настроить на обработку неслучайных совокупностей ключей, а трехпутевая быстрая сортировка идеально подходит для случаев, когда преобладают дублированные ключи.

Как и в случае быстрой сортировки, структуру разделения удобно описывать в виде бинарного дерева (аналогично тому, как она представлена на рис. 10.4): корень дерева соответствует подфайлу, подвергаюше-муся сортировке, а два его поддерева - двум подфайлам, полученным в результате выполнения разделения. Мы, по крайней мере, знаем, что в результате выполнения стандартной быстрой сортировки одна из записей помешается в процессе разделения в свою окончательную позицию, следовательно, помещаем этот ключ в корневой узел; мы знаем также, что в условиях бинарной сортировки ключи попадают в свои окончательные позиции, только когда мы доходим до подфайлов размером 1, либо когда все разряды ключа исчерпаны; таким образом, мы помещаем эти ключи на нижний уровень дерева. Такая структура назы-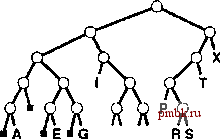

LMNO

РИСУНОК 10.4. ДЕРЕВО РАЗДЕЛЕНИЯ ДЛЯ ДВОИЧНОЙ БЫСТРОЙ СОРТИРОВКИ

Это дерево описывает структуру разделения для двоичной быстрой сортировки, соответствующей рис. 10.2 и 10.3. Поскольку нет гарантии того, что какие-либо элементы займут свои окончательные позиции, ключи соответствуют внешним узлам дерева. Такая структура обладает следующим свойством: продвигаясь по пути от корня к конкретному ключу, принимая О за левую ветвь и I за правую ветвь, получаем значения старших разрядов этого ключа. Именно эти значения и отличают данный ключ от всех остальных во время сортировки. Маленькие черные квадраты представляют нулевые разделения (когда все ключи переходят на другую сторону, поскольку значения старших разрядов совпадают). В условиях рассматриваемого примера это может случиться только в окрестности нижнего уровня дерева, однако возможно и на более высоких уровнях: например, если Тили Хв число таких ключей не входили, то их узлы на чертеже будут заменены нулевым узлом. Обратите внимание на тот факт, что дублированные ключи (Аи Е) не могут быть разделены (сортировка поставит их в один подфайл только после исчерпания всех их битов).

вается бинарным деревом (trie); свойства такого бинарного дерева подробно анализируются в главе 15. Например, одно из таких свойств, представляющих несомненный интерес, заключается в том, что структура бинарного дерева полностью определяется значениями ключей, а не порядком их следования.

Разделы, получаемые в процессе выполнения быстрой сортировки, зависят от двоичного представления и числа сортируемых элементов. Например, если файлы представляют собой случайные перестановки целых чисел, меньших 171 = 1010101Ь, то разделение по первому биту эквивалентно разбиению по значению 128, так что получаем неравные подфайлы (один файл размером 128, а другой размером 43). Ключи на рис, 10.5 суть произвольные 8-разрядные значения, таким образом, этот эффект в рассматриваемом случае не имеет места, однако он достоин того, чтобы на него обратить внимание сейчас, чтобы он не стал для неприятным сюрпризом, когда мы столкнемся с ним на практике.

Мы можем внести усоверщенствования в базовую рекурсивную реализацию, представленную программой 10.1, за счет отказа от рекурсии и обработки подфайлов небольших размеров другим способом, как это делалось в случае стандартной быстрой сортировки в главе 7.

Упражнения

[>10.8. Начертите дерево в стиле рис. 10.2, которое соответствует процессу разделения в поразрядной быстрой сортировке, для ключей EASYQUESTION.

10.9. Сравните число операций обмена местами, используемых при двоичной быстрой сортировке с аналогичным показателем обычной быстрой сортировки для 3-разрядных двоичных чисел 001, 011, 101, 110, ООО, 001, 010, 111, ПО, 010.

о 10.10. Почему сортировка меньшего из двух подфайлов первым менее важна в случае двоичной быстрой сортировки, чем в случае обычной быстрой сортировки?

о 10.11. Опишите, что произойдет на втором уровне разделения (когда левый подфайл подвергается разделению и когда правый подфайл подвергается разделению), в случае применения двоичной быстрой сортировки для упорядочения случайных перестановок неотрицательных целых чисел, меньших 171.

10.12. Написать программу, которая на проходе, предшествующем процессу обработки, определяет число старших разрядов, на которых все ключи равны, затем вызывает

РИСУНОК 10.5. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВОИЧНОЙ БЫСТРОЙ СОРТИРОВКИ НА КРУПНОМ ФАЙЛЕ Разбиения на части при двоичной быстрой сортировке менее чувствительны к порядку расположения ключи, чем в условиях стандартной быстрой сортировки. В рассматриваемом случае выполнение этой процедуры на двух различных 8-разрядный файлах с произвольной организацией приводят к практически идентичным профилям разделений.