Указанные рамки производительности служат целью разработки соответствующей структуры данных. Они представляют собой последствия того факта, что во всех реализациях имеется один или два цикла, которые выполняют итерацию на корнях деревьев биномиальной очереди.

Программа 9.16. Объединение (слияние) двух биномиальных очередей

Данная программа моделирует арифметическую операцию сложения двух двоичных чисел. Продвигаясь справа налево с начальным значением разряда переноса, равным О, принимается во внимание три возможных случая (учитываются все возможные значения операндов и разряда переноса). Например, случай 3 соответствует условиям, когда биты обоих операндов принимают значения 1, а бит переноса - значение 0. В этом случае результатом будет О, но перенос принимает значение 1 (т.е., результат сложения значений разрядов операндов).

Подобно функции pair, рассматриваемая функция является приватной функцией-членом реализации, которая вызывается функциями getmax и join. Функция абстрактного типа данных Join(PQ<ltein>& р) реализована в виде вызова BQJoin(bq, p.bq).

static inline int te8t( int C, int B, int A)

{return 4*C + 2*B + 1*A} static void BQjoin (link *a, link *b)

{ link с = 0;

for (int 1 = 0; 1 < maxBQsize; i++)

switch(test(c

case 2:

case 3:

case 4:

case 5:

case 6:

case 7:

!= 0; b[i] !- 0, a[i] = 0))

a[i] = b[i] ; break; с = pair (a [i], b[il); a[i] = 0; break; a[i] c, с =0; break; с = pair(с, a[i]); a[i] = 0; break;

С = pair(с, b[i]); break;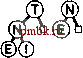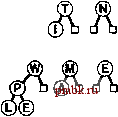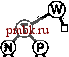

РИСУНОК 2.20. ОБЪЕДИНЕНИЕ ДВУХ БИНОМИАЛЬНЫХ ОЧЕРЕДЕЙ

Добавление биномиальной очереди из 3 узлов к биномиальной очереди из 7узлов имеет своим результатом очередь из 10 узлов как результат выполнения процесса, который моделирует операцию сложения 0\\+\\\=\0Щ двоичной арифметики. Сложение N и Е дает пустое 1-дерево и перенос 2-дерева, содержащего узлы N и Е. Последующее сложение трех 2-деревьев оставляет одно из них в итоговой очереди, а в перенос попадает 4-дерево, содержащее узлы TNEI. Это 4-дерево складывается с другим 4-деревом, образуя биномиальную очередь, показанную в нижней части диаграммы. Процесс охватывает небольшое количество узлов.

В целях упрощения будем считать, что наши реализации проходят в цикле через все деревья, так что время их выполнения пропорционально логарифму максимального размера биномиальной очереди. Можно сделать так, чтобы эти реализации соответствовали указанным фаничным значениям в тех случаях, когда фактический размер очереди намного меньше, чем ее максимальный размер, путем отслеживания размеров очереди или за счет выбора соответствующего значения сигнальной метки, отмечающей точки, в которых циклы должны прекратиться (см. упражнения 9.61 и 9.62). Во многих ситуациях результат внесения подобного рода изменений не стоит

затраченных на них усилий, поскольку максимальный размер очереди экспоненциально превосходит максимальное число итераций циклов. Например, если в качестве максимального размера очереди принимается 2, а количество элементов очереди обычно выражается тысячами, то простейшие из реализаций будут повторять цикл 15 раз, в то время как более сложные методы снижают число повторений цикла всего лишь до И или 12, при этом на поддержание максимального размера очереди и сигнальной метки требуется дополнительный расход ресурсов. С другой стороны, безосновательный выбор большого значения максимума может привести к тому, что на очередях малых размеров программы начнут работать медленнее, нежели рассчитывалось.

Лемма 9.8. Построение биномиальной очереди с выполнением N операций вставок в первоначально пустую очередь требует выполнения 0{N) сравнений в наихудшем случае.

Для одной половины вставок (когда размер очереди представлен четным числом и 1-деревья отсутствуют) операции сравнения вообще не требуются; для половины оставшихся вставок (если нет 2-деревьев) требуется лишь одна операция сравнения; если нет 4-деревьев, требуется только 2 операции сравнения и т.д. Следовательно, обшее число сравнений меньше О N/ 2 + 1 N/4 + 2 N/ S +... < N. Что касается леммы 9.7, то нам нужна одна из модификаций из числа тех, которые рассматривались в упражнениях 9.61 и 9.62, чтобы получить в наихудшем случае время выполнения, не превышающее линейного.

Как уже упоминалось в разделе 4.8, мы не рассматривали вопросов распределения памяти при реализации операции объединить в программе 9.16. В силу этой причины при выполнении операции имеет место утечка памяти, так что в некоторых ситуациях она становится непригодной. Для исправления этого дефекта потребуется уделить соответствующее внимание вопросу распределения памяти под аргументы и возвращаемое значение функции, которая реализует операцию объединить (см. упражнение 9.65).

Для биномиальных очередей характерно высокое быстродействие, тем не менее, были предложены специальные структуры данных, которые обладали в теоретическом плане еще лучшими характеристиками, гарантировано обеспечивая постоянное время выполнения некоторых операций. Эта проблема вызывает интерес и предлагает разработчиками структур данных широкое поле деятельности. С другой стороны, практическое применение многих из этих, понятных только посвященным, структур весьма сомнительно, а мы должны знать, что от некоторых имеющих место ограничений эффективности можно избавиться только путем снижения времени выполнения некоторых операций на очередях по приоритетам, прежде чем пускаться на поиски сложных решений в области структур данных. И в самом деле, для практических применений предпочтение следует отдавать тривиальным структурам при отладке и при работе с очередями малых размеров; далее, для ускорения операций, если речь не идет о получении быстродействующей операции объединить, необходимо использовать сортирующие деревья. Наконец, биномиальными очередями следует пользоваться, если требуется получить логарифмическое время выполнения всех операций. Однако, принимая во внимание все сопутствующие факторы, приходим к выводу, что пакет очередей по приоритетам на базе биномиальных очередей является, несомненно, ценным вкладом в библиотеку программного обеспечения.

Упражнения

t> 9.54. Вычертить биномиальную очередь размера 29, воспользовавшись представлением в виде биномиального дерева.

9.55. Напишите программу построения представления биномиальной очереди в виде биномиального дерева заданного размера N (только узлы, соединенные ребрами, но не ключи).

9.56. Построить биномиальную очередь, которая получится, если ключи EASY QUESTION вставляются в первоначально пустую биномиальную очередь.

9.57. Построить биномиальную очередь, которая получится, если ключи EASY вставляются в первоначально пустую биномиальную очередь, и построить биномиальную очередь, которая получится, если вставить ключи QUESTIONb первоначально пустую очередь. Затем выполните операцию удалить наибольший в обеих очередях и представьте результат. И наконец, представьте результат выполнения операции объединить применительно к полученным очередям.

9.58. Используя соглашения из упражнения 9.1, построить последовательность биномиальных очередей, полученных в результате того, что операции PRIO*R**I*T*Y***QUE***U*E выполняются на первоначально пустой биномиальной очереди.

9.59. Используя соглашения из упражнения 9.1, построить последовательность биномиальных очередей, полученных в результате того, что операции

(((PRIO*) + (R *IT*Y*))***)+ (QUE***U*E)

выполняются на первоначально пустой биномиальной очереди.

9.60. Доказать, что биномиальное дерево с 2 узлами имеет . узлов на уровне

/, причем О < / < . (Этот факт и послужил причиной того, что подобного рода структура данных получила название биномиального дерева).

о 9.61. Построить такую программную реализацию биномиальной очереди, чтобы выполнялась лемма 9.7, внося изменение в тип данных биномиальной очереди, чтобы он содержал размер этой очереди с целью последующего использования этого значения для управления циклами.

о 9.62. Построить такую программную реализацию биномиальной очереди, чтобы выполнялась лемма 9.7. Использовать для этой цели сигнальный указатель, отмечающий точку, в которой циклы должны завершаться.

9.63. Реализовать операцию вставить (insert) для биномиальных очередей путем явного использованием одной лишь операции объединить Qoin).

9.64. Реализовать операцию изменить приоритет (change priority) и удалить (remove) для биномиальных очередей. Совет: Потребуется добавить третью связь, которая указывает на узлы вверх по дереву.