Программа 9.14. Ваавка в биномиальную очередь

Для вставки узла в биномиальную очередь его сначала потребуется превратить в 1-дерево и идентифицировать как сортирующее 1-дерево переноса, а затем повторять в цикле следующий процесс, начиная с / = 0. Если в биномиальной очереди сортирующее 2-дерево отсутствует, в очередь помещается 2-дерево переноса. Если в биномиальной очереди такое дерево есть, оно объединяется с таким же новым деревом (с применением функции pair из программы 9.13) и получается 2-дерево, после чего значение / увеличивается на 1 и процесс продолжается до тех пор, пока не обнаруживается пустая позиция для сортирующего дерева в биномиальной очереди.

handle insert (Item)

{ link t = new node(v), с = t;

for (int i = C; i < maxBQsize; i++) {

if (c == C) break; if (bq[i] == C)

{ bq[i] = c; break; } с = pair(с, bq[i]); bq[i] = C;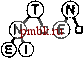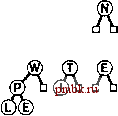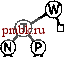

return t;

РИСУНОК 9.17. ВСТАВКА НОВОГО ЭЛЕМЕНТА В БИНОМИАЛЬНУЮ ОЧЕРЕДЬ

Добавление элемента в биномиальную очередь из семи узлов аналогично выполнению арифметической операции двоичного сложения 1112+ 1 =

lOOOj с переносом в каждом разряде. В результате получаем биномиальную очередь, представленную в нижней части диаграммы и состоящую из 8-дерева, причем 4-, 2- и 1-деревья отсутствуют.

Другие операции, выполняющиеся в биномиальных очередях, понять проще, если сравнить их с операциями двоичной арифметики. Как мы вскоре убедимся, реализация операции объединить соответствует реализации операции сложения двоичных чисел.

Предположим на момент, что в нащем распоряжении имеется (эффективная) функция для операции объединить Ooin), предназначенная для слияния очереди по приоритетам, ссылка на которую передается во втором операнде функции, с очередью по приоритетам, ссылка на которую находится в первом операнде (результат выполнения операции сохраняется в первом операнде). С использованием этой функции можно реализовать операцию вставить (insert) за счет вызова функции объединить, в одной из операндов которой передается биномиальная очередь размером 1 (см. упражнение 9.63).

Можно также реализовать операцию удалить наибольший (remove the maximum) путем одного вызова операции объединить. Для нахождения максимального элемента в биномиальной очереди просматриваются сортирующие деревья степени 2 этой очереди. Каждое такое дерево - левостороннее пирамидально упорядоченное сортирующее дерево, следовательно, максимальный его элемент находится в корне. Больший из корневых элементов является наибольшим элементом биномиальной очереди. Поскольку в биномиальной очереди не может быть более IgAдеревьев, общее время поиска наибольшего элемента меньше IgA.

Программа 9.15. Удаление наибольшего элемента из биномиальной очереди

Сначала производится просмотр корневых узлов, чтобы выяснить, какой из них больше, затем из биномиальной очереди удаляется сортирующее дерево степени 2, содержащее наибольший элемент. Далее из сортирующего дерева степени 2 удаляется корневой узел, содержащий наибольший элемент, и временно строится биномиальная очередь, которая содержит остальные составляющие части сортирующего дерева степени 2. В завершение при помощи операции объединить выполняется слияние полученной таким путем биномиальной очереди и исходной биномиальной очереди.

Item getmax( )

{ int i, max; Item v = 0;

link* temp = new link [maxBQsize] ; for ( i = 0, max = -1; i < maxBQsize; i++) if ( bq[i] !=0)

if ((max == -1) II (v < bq[i]->item)) { max = i; v = bq[max]->item; } link X = bq[max]->l;

for (i = max; i < maxBQsize; i++) temp[i] = 0; for (i = max; i > 0; i-) { temp[i-1] = x;

X = x->r;

ten5>[i-l]->r = 0;

delete bq[max] ; bq[max] = 0; BQjoin (bq, temp); delete tBwp; return v;

Перед выполнением операции удалить наибольший (remove the maximum) потребуется отметить, что удаление корня левостороннего сортирующего 2*-дерева приводит к появлению к левосторонних сортирующих деревьев степени 2 - 2* -дерево, 2*~-дерево и так далее - которые легко реструктурировать в биномиальную очередь размера 2*-1, как показано на рис. 9.18. Затем можно воспользоваться операцией объединить, чтобы объединить биномиальную очередь с остальной частью исходной очереди с целью заверщения операции удалить наибольший. Эта реализация показана в профамме 9.15.

Каким образом объединяются две биномиальных очереди? Прежде всего, следует отметить, что эта операция тривиальна, если обе очереди не содержат сортирующих деревьев степени 2 одинакового размера, как показано на рис.9.19; мы просто выполняем слияние деревьев из обеих биномиальных очередей и получаем одну биномиальную очередь. Очередь размера 10 (состоящая из 8-дерева и 2-дерева) и очередь размера 5 (состоящая из 4-дерева и 1-дерева) путем простого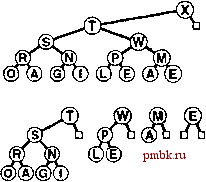

РИСУНОК 9.18. УДАЛЕНИЕ НАИБОЛЬШЕГО ЭЛЕМЕНТА ИЗ СОРТИРУЮЩЕГО ДЕРЕВА СТЕПЕНИ 2.

Убрав корень, получаем бор сортирующих деревьев степени 2; все они левосторонне пирамидально упорядочены, при этом их корни берутся из правого ствола дерева. Эта операция позволяет найти способ удаления наибольшего элемента из биномиальной очереди: убираем корень сортирующего дерева степени 2, которое содержит наибольший элемент, затем выполняем операцию объединить для слияния полученной биномиальной очереди с остальными сортирующими деревьями степени 2 исходной биномиальной очереди.

0:ожо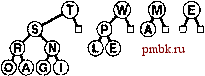

□

слияния образуют очередь размера 15 (состоящую из 8-дерева, 4-дерева, 2-дерева и 1-дерева). Способ, рассчитанный на более общие случаи, выполняется по прямой аналогии со сложением двух двоичных чисел, дополненного переносом (см. рис. 9.20).

Например, если очередь размером 7 (состоящую из 4-дерева, 2-дерева и 1-дерева) добавить к очереди размером 3 (состоящую из 2-дерева и 1-дерева), получится очередь размером 10 (состоящая из 8-дерева и 2-дерева). Для сложения потребуется слить 1-деревья и выполнить перенос 2-дерева, затем слить 2-деревья и выполнить перенос 4-дерева, затем слить 4-деревья, чтобы в результате получить 8-дерево точно таким же способом, каким выполняется двоичное сложение OII2+ ПЬЮЮг. Пример, представленный на рис. 9.19, проще примера, показанного на рис. 9.20, поскольку он аналогичен операции сложения 10102 + 01012=11112-

Столь непосредственная аналогия с операциями двоичной арифметики вплотную подводит к естественной реализации операции объединить (см. программу 9.16). Для каждого разряда приходится рассматривать восемь возможных случаев в зависимости от значения каждого из 3 разрядов (перенос и два разряда в операндах). Соответствующая программа ненамного сложнее, чем программа простого арифметического сложения, поскольку в этом случае мы имеем дело с четко различимыми сортирующими деревьями, а не с неразличимыми битами, однако в обоих случаях принципиальных трудностей не возникает. Например, если все три разряда принимают значения 1, мы должны оставить одно дерево в получающейся биномиальной очереди, а два других объединить и перенести в следующую позицию. В самом деле, эта операция предоставляет полный цикл на абстрактных типах данных: мы (открыто) противимся искушению перевести программу 9.16 в статус абстрактной двоичной дополнительной процедуры, в рамках которых реализация биномиальной очереди есть ни что иное, как клиентская программа, использующая более сложную процедуру сложения битов, представленную программой 9.13.

Лемма 9.7. Все операции на очереди по приоритетам как на абстрактном типе данных могут быть реализованы на биномиальной очереди таким образом, что для выполнения любой из них на очереди из N элементов требуется 0(lgAO шагов.

РИСУНОК 9.19. ОБЪЕДИНЕНИЕ ДВУХ БИНОМИАЛЬНЫХ ОЧЕРЕДЕЙ (БЕЗ ПЕРЕНОСА)

В том случае, когда две объединяемые биномиальные очереди содержат только сортирующие деревья степени 2, размеры которых попарно различны, операция объединения есть ни что иное как слияние. Выполнение этой операции аналогично сложению двух двоичных чисел, в условиях которой не встречаются сложения типа 1 +1 (т.е. без переносов). В рассматриваемом случае биномиальная очередь из 10 узлов сливается с очередью из 5 узлов, результатом чего является биномиальная очередь из 15 yxioe, соответствующая операции 10102+0101= 11 П.