рядоченных дерева, но как слить их в одно? Например, если одно из этих деревьев содержит 1023 узла, а другое - всего лишь 255 узлов, то какой способ выбрать для их слияния, чтобы получить дерево из 1278 узлов, не затрагивая более 10 или 20 узлов? На первый взгляд задача слияния пирамидально упорядоченных деревьев кажется вообще невозможной, если эти деревья являются пирамидально упорядоченными и полными, тем не менее, были предложены различные более совершенные структуры данных, которые позволили ослабить условия пирамидальной упорядоченности и сбалансированности с тем, чтобы придать структурам данных большую гибкость, необходимую для получения эффективной реализации операции объединить. Далее мы рассмотрим оригинальное решение этой проблемы, получившее название биномиальной очереди, полученное Вильемином (Vuillemin) в 1978 г.

Вначале следует отметить, что операция объединить Coin) тривиальна для одного специального типа дерева с ослабленным требованием необходимости быть пирамидально упорядоченным.

Определение 9.4. Бинарное дерево, содержащее узлы с ключами, называется левосторонним пирамидально упорядоченным (left heap ordered), если ключ каждого узла больше или равен всем ключам левого поддерева этого ключа (если таковое имеется).

Определение 9.5. Сортирующее дерево степени 2 есть левостороннее пирамидально упорядоченное дерево, состоящее из корневого узла с пустым правым поддеревом и полным левым поддеревом. В дереве, соответствующем сортирующему дереву степени 2 по левому потомку, соответствие правому потомку называется биномиальным деревом (binomial tree).

Биномиальные деревья и сортирующие деревья степени 2 эквивалентны. Мы будем работать с обоими представлениями, поскольку в своем воображении несколько легче построить зрительный образ биномиальные дерева, в то время как упрощенное представление сортирующих деревьев степени 2 приводит к более простой реализации. В частности, мы ощущаем свою зависимость от следующих факторов, являющихся прямым следствием приведенных определений:

Количество узлов сортирующего дерева степени 2 есть степень числа 2.

Ни один из узлов не обладает ключом, который превосходит по значению ключ корня.

Биномиальные деревья пирамидально упорядочены.

Тривиальной операцией, на которой базируются все биномиальные алгоритмы, является объединение двух сортирующих деревьев степени 2, состоящих из одинакового числа узлов. В результате объединения получаем сортирующее дерево, содержащее в два раза большее число узлов, которое, как показано на рис. 9.16, совсем нетрудно построить. Корневой узел с большим значением ключа становится корнем результирующего дерева (другой исходный корень при этом становится потомком корня результирующего дерева), а его левое поддерево становится правым поддеревом другого корневого узла. Если задано связное представление деревьев, то операция объединения выполняется за постоянное время: мы всего лишь устанавливаем две связи в вершине. Программная реализация этой операции находится в программе 9.13. Эта базовая операция является центральным звеном общего решения пробле-

мы реализации очереди по приоритетам без единой медленной операции, предложенного Виллемином (Vuillemin).

Определение 9.6. Биномиальная очередь представляет собой набор сортирующих деревьев степени 2, ни одно из которых не совпадает с остальными по размеру. Структура биномиальной очереди определяется числом узлов этой очереди в соответствии с двоичным представлением целых чисел.

Биномиальная очередь из элементов содержит по одному сортирующему дереву на каждый бит двоичного представления числа N. Например, биномиальная очередь из 13 узлов содержит одно 8-узловое сортирующего дерево, одно 4-узловое и одно 1-узловое дерево (см. рис, 9.15), В биномиальной очереди размера содержатся максимум IgA сортирующих деревьев степени 2, высота которых не превосходит значения IgA,

В соответствии с определениями 9.5 и 9,6, сортирующие деревья степени 2 (и дескрипторы элементов данных) представляются как связи с узлами, содержащими ключ и две связи каждый (подобно явному древовидному представлению турниров на рис. 5.10), а биномиальные очереди представляются как массивы сортирующих деревьев степени 2 путем включения следующего кода в приватную часть программы 9.8:

struct node

{ Item item; node *1, *r; node(Item v)

{ item = v; 1 = 0; r = 0; }

typedef node *linlc; link* bq;

Программа 9.13. Объединение двух сортирующих деревьев аепени 2 одинаковых размеров

®Щ (D©

©:©жо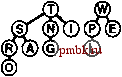

РИСУНОК 9.15. БИНОМИАЛЬНАЯ ОЧЕРЕДЬ РАЗМЕРА 13

Биномиальная очередь размера N представляет собой список левосторонних пирамидально упорядоченных сортирующих деревьев степеней 2, по одному на каждый бит двоичного представления числа N. Таким образом, биномиальная очередь размера 13 = 1101 состоит из одного 8-узлового сортирующего дерева, одного 4-узлового и одного 1-узлового деревьев. На диаграмме показано представление в виде левостороннего пирамидально упорядоченного сортирующего дерева степеней 2 (сверху) и представление в виде биномиального пирамидально упорядоченного дерева (внизу) одной и той же биномиальной очереди.

Чтобы объединить два сортирующих дерева степени 2 одинаковых размеров в одно сортирующее дерево степени 2 двойного размера достаточно изменить лишь несколько связей. Эта функция, которая в реализации определена как приватная функция-член, представляет собой ключевой фактор, обеспечивающий эффективность алгоритма биномиальной очереди.

static link pair(link p, link q)

if (p->item < q -> item)

{ p->r = q->l; q->l = p; return q; } else {q->r = p->l; p->l = q; return q; }

Размеры массивов невелики и высота деревьев тоже, а само это представление обладает достаточной гибкостью, чтобы стала возможной реализация всех операций с очередями по приоритетам менее чем за IgiV шагов, как мы в этом сейчас убедимся.

Начнем с рассмотрения операции вставить (insert). Процесс вставки нового элемента в биномиальную очередь в точности отображает процесс увеличения значения двоичного числа на единицу. Чтобы увеличить значения двоичного числа на единицу, мы двигаемся справа налево, заменяя 1 на О в силу необходимости выполнения переноса, обусловленного тем, что 1 + 1 = Юг, пока не обнаружим О в самой правой позиции, который заменяем единицей. Аналогичным образом, чтобы добавить в биномиальную очередь новый элемент, мы продвигаемся справа налево, выполняя слияние сортирующих деревьев, соответствующих битам 1 с переносимым сортирующим деревом, пока не найдем самую правую пустую позицию, в которую и помещаем переносимое дерево.

В частности, для вставки нового элемента в биномиальную очередь мы превращаем новый элемент в 1-узловое сортирующее дерево. Далее, если N есть четное число (значение самого правого разряда равно 0), мы просто помещаем это сортирующее дерево в самую правую пустую позицию биномиальной очереди. Если N - нечетное число (значение самого правого разряда составляет 1), мы объединяем сортирующее 1-дерево, соответствующее новому элементу, с сортирующим 1-деревом в самой крайней правой позиции биномиальной очереди, в результате чего получаем сортирующее 2-дерево переноса. Если позиция, соответствующая 2 в биномиальной очереди, пуста, то сортирующее дерево переноса помещается в эту позицию, в противном случае производится слияние сортирующего 2-дерева переноса с сортирующим 2 деревом из биномиальной очереди, образуя при этом 4-дерево переноса, и так продолжая процесс до тех пор, пока не будет достигнута пустая позиция в биномиальной очереди. Этот процесс демонстрируется на рис. 9.17, а в профамме 9.14 приведена его реализация.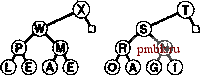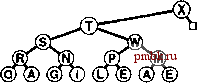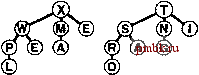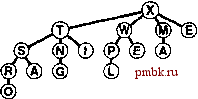

РИСУНОК 9.16. ОБЪЕДИНЕНИЕ ДВУХ СОРТИРУЮЩИХ ДЕРЕВЬЕВ СТЕПЕНИ 2 ОДИНАКОВОГО РАЗМЕРА

Мы объединяем два сортирующих деревьев степени 2 (сверху), помещая больший из двух корней в вершину результирующего дерева, при этом поддерево (левое) этого корня становится правым поддеревом другого исходного корня. Если операнды содержат 2 узлов, то результат содержит 2 * узлов. Если операндами являются пирамидально упорядоченные левосторонние деревья, такой же порядок сохраняется и в результирующем сортирующем дереве, при этом ключ с наибольшим значением находится в корне. Отображение той же операции, ориентированной на представление пирамидально упорядоченного биномиального дерева, показано под разделительной чертой.