9.42. Добавить реализацию (решение в лоб ) операции объединить в реализацию из упражнения 9.41.

о 9.43. Добавить объявления деструктора, конструктора копирования и перегруженный оператор присваивания в программу 9.8, чтобы превратить ее в АТД первого класса, включить соответствующие реализации в программы 9.9 и 9.10 и написать программу-драйвер, которая протестирует полученные интерфейс и реализацию.

9.44. Внести изменения в интерфейс и реализацию операции объединить в профаммы 9.9 и 9.10, которые приведут к тому,

что она возвращает PQ (результат объединения параметров) и имеет своим результатом разрушение аргументов.

9.45. Построить интерфейс очереди по приоритетам и реализацию, которая поддерживает операции построить и удалить наибольший, используя для этой цели турнир (см. раздел 5.7). Программа 5.19 обеспечивает основу для операции построить (construct).

9.46. Преобразовать решение упражнения 9.45 в АТД первого класса.

9.47. Добавить операцию вставить в решение упражнения 9.45.

It ЯрСк] pqCk] data [к]

9.6. Очередь по приоритетам для индексных элементов

Предположим, что записи, обрабатываемые в очередях по приоритетам, образуют массив. В этом случае программам, работающим с очередями по приоритетам, имеет смысл обращаться к элементам, используя индексы массивов. Более того, индексы массива могут рассматриваться в качестве дескрипторов, чтобы реализовать все операции, выполняемые над очередями по приоритетам. Интерфейс, соответствующий этому описанию, приводится в программе 9.11. Рисунок 9.13 демонстрирует, как такой подход можно применить в примере, который использовался для изучения индексной сортировки в главе 6. Обходясь без копирования и не внося специальных изменений в записи, можно поддерживать очередь по приоритетам, содержащую некоторое подмножество записей.

РИСУНОК 9.13. СТРУКТУРЫ ДАННЫХ ИНДЕКСНОГО СОРТИРУЮЩЕГО ДЕРЕВА

Манипулируя индексами, а не самими записями, можно построить очередь по приоритетам на подмножестве записей в массиве. В рассматриваемом случае сортирующее дерево размером 5 в массиве pq содержит имена 5 студентов с наивысшими рейтингами. Таким образом, data[pq[l]].name содержит Smith, имя студента, обладающего наивысшим рейтингом, и т.д. Обращенный массив позволяет программам очереди по приоритетам трактовать индексы массива как дескрипторы. Например, если требуется поменять индекс Смита на 85, мы меняем содержимое data[3].grade, затем вызываем функцию PQchange(3). Реализация очереди по приоритетам осуществляет доступ к записи pq[qp[3]] в (или pq[l], поскольку qp[3]=l и к новому ключу в data[pq[l]].name (или data[3] .name, поскольку pq[ 1 ]=3/

Использование индексов существующего массива - вполне естественное рещение, однако оно ведет к реализациям с ориентацией, противоположной программе 9.8. Теперь уже клиентская программа не может свободно перемещаться по информации, поскольку программа, реализующая очередь по приоритетам, работает с теми же индексами, с которыми имеет дело и клиентская профамма. В свою очередь, реализация очереди по приоритетам должна пользоваться индексами только в тех случаях, когда они сначала передаются ей клиентской программой.

При разработке реализации применяется в точности такой же подход, который использовался при индексной сортировке в разделе 6.8. Мы манипулируем индексами и перегружаем операцию operator< таким образом, что сравнения адресуются к элементам массива индексов клиентской программы. При этом возникают некоторые осложнения, поскольку необходимо, чтобы программа очереди по приоритетам отслеживала объекты так, чтобы она могла отыскать их, когда клиентская программа обращается к ним по дескриптору (индексу массива). С этой целью добавляется второй индексный массив, обеспечивающий отслеживание положения ключей в очереди по приоритетам. Чтобы локализовать поддержку этого массива, данные перемещаются только через операцию exch, поэтому необходимо дать соответствующее определение exch.

Полная реализация этого подхода с использованием сортирующих деревьев находится в программе 9.12. Эта программа только незначительно отличается от программы 9.5, тем не менее, она достойна специального изучения, поскольку является исключительно полезной в практических ситуациях. Будем называть сфуктуру данных, построенную этой профаммой, индексным сортирующим деревом (index heap). Эта профамма служит строительным блоком для других алгоритмов в частях 5-7. Как обычно, мы не включаем код обнаружения ошибок и предполагаем (например), что индексы никогда не выходят за пределы отведенного им диапазона, а пользователь не делает попыток вставить что-либо в заполненную очередь и удалить что-либо из пустой очереди. Добавление кода подобного назначения не вызывает особых зафудне-ний.

Программа 9.11. Интерфейс АТД очереди по приоритетам для индексных элементов.

Вместо того чтобы строить различные структуры данных из самих элементов данных, этот интерфейс обеспечивает возможность построения очереди по приоритетам с использованием индексов конкретных элементов массива клиентской программы. Программы, реализующие операции вставить, удалить наибольший, изменить приоритеты и удалить, используют дескриптор, представляющий собой индекс массива, а клиентская программа перегружает операцию operatoK так, чтобы стало возможным сравнение двух элементов массива. Например, клиентская программа может определить operator< таким образом, что значением неравенства i < j становится результат сравнения data[i].grade и data[j].grade.

template <class Item> class PQ {

private:

Программный ход, аависвпций от реализации pxiblic:

PQ(int) ;

int empty{) const;

Распечатано программой Firii

void insert(Index) ; Index getmax(); void change(Index); void remove(Index);

Этот же подход применим и для любой очереди по приоритетам, для которой используется представление в виде массива (например, см. упражнения 9.50 и 9.51). Основной недостаток применения подобного рода косвенной адресации состоит в необходимости расхода дополнительного объема памяти. Размер массива индексов должен иметь размер массива данных, тогда как максимальный размер очереди по приоритетам может быть намного меньше. Другой подход к построению очереди по приоритетам над данными, образующими массив, заключается в том, чтобы клиентская программа строила записи, состоящие из ключа и индекса массива в качестве дополнительной информации, или в использовании индексного ключа с перегруженной операцией operator<, поддерживаемой клиентской программой. Далее, если рассматриваемая реализация использует представление со списочным распределением памяти, такое как в программах 9.9 и 9.10 или в упражнении 9.41, то пространство памяти, используемое очередью по приоритетам, будет пропорционально максимальному количеству элементов в очереди в каждый конкретный момент времени. Такого рода подходы по сравнению с подходом, примененным в профамме 9.12, выглядит предпочтительнее, если заранее нужно зарезервировать определенное пространство памяти необходимо заранее или если очередь по приоритетам включает в себя только небольшую часть массива данных.

Программа 9.12. Очередь по приоритетам, поароенная на базе индексного сортирующего дерева

Эта реализация программы 9.11 поддерживает pq как массив индексов некоторого клиентского массива. Например, если клиент определяет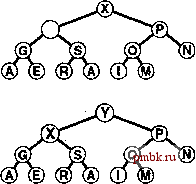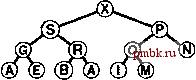

РИСУНОК 9.14. ИЗМЕНЕНИЕ ПРИОРИТЕТА ПРОИЗВОЛЬНОГО УЗЛА СОРТИРУЮЩЕГО ДЕРЕВА

На верхней диаграмме показано copmupywutee дереве, о котором известно, что оно пирамидально упорядоченно, за исключением разве что одного узла. Если этот узел больше своего родителя, то он должен продвинуться вверх, как показано на рис. 9.3. Эта ситуация демонстрируется и на средней диаграмме; в рассматриваемом случае узел Y поднимается вверх по дереву (в общем случае его продвижение может прекратиться, так и не достигнув корня). Если узел меньше, чем больший из его двух потомков, то он должен опуститься вниз по дереву, как показано на рис. 9.3. Эта иллюстрация показана на нижней диаграмме, в этом случае узел В продвигается вниз по дереву (в общем случае его продвижение может прекратиться, так и не достигнув нижнего уровня). Данной процедурой можно воспользоваться в качестве основы для операции изменить приоритет в сортирующем дереве с целью восстановления структуры сортирующего дерева после изменения значения ключа в узле, либо в качестве основы для операции удалить в сортирующем дереве с целью восстановления структуры сортирующего дерева после замены ключа в узле на самый правый ключ нижнего уровня дерева.