Лемма 9.6. Выборка на базе пирамидальной сортировки позволяет отыскать к-й наибольший элемент из N элементов за время, пропорциональное N, когда к мало или близко по величине к N, либо за время, пропорциональное N logN, во всех других случаях.

Один метод заключается в том, чтобы построить сортирующее дерево с использованием числа операций сравнения меньшего 2N (см. лемму 9.4), с последующим удалением к наибольших элементов, используя для этой цели 2k\%N или меньшее количество операций сравнения (см. лемму 9.4), при общем числе сравнений, равном 2N + 2к \gN. Другой метод связан с построением минимально ориентированного сортирующего дерева размером к с последующим выполнением операции заменить наименьший (replace the minimum) (операция вставить плюс операция удалить наименьший) на оставшихся элементах, при общем количестве операций сравнения, не превосходящем 2к + 2(Л -A;)lgA; (см. упражнение 9.36). Этот метод использует дополнительную память, пропорциональную к, и является особо привлекательным для нахождения к наибольших из Л элементов в условиях, когда к принимает малое, а N - большое значение (или ничего не известно заранее). Что касается случайных ключей или других типичных ситуаций верхняя граница \gk для операций на сортирующем дереве во втором методе, по-видимому, есть 0(1), когда к мало по сравнению с N (см. упражнение 9.36).

Исследованы другие способы дальнейшего улучшения пирамидальной сортировки. Одна из идей, развитая Флойдом, состоит в использовании того обстоятельства, что элемент, повторно вставляемый в процессе нисходящей сортировки, проделывает весь путь на нижний уровень, так что мы можем сэкономить время, затрачиваемое на проверку достижения таким элементом своей позиции, просто продвигая больший из двух потомков до тех пор, пока не будет достигнут нижний уровень с последующим продвижением вверх по сортирующему дереву в соответствующую позицию. Благодаря этой идее коэффициент сокращения числа выполняемых операций сравнения асимптотически стремится к 2 и принимает значение, близкое к IgA! = NlgN- N/ 1п2, что является абсолютным минимумом количества сравнений для любого алгоритма сортировки (см. часть 8). Этот метод требует дополнительных вычислений и может оказаться полезным на практике только в ситуациях, когда расходы на операции сравнения сравнительно велики (например, при сортировке записей со строковыми с ключами или другими видами длинных ключей).

Другая идея заключается в том, чтобы построить сортирующие деревья, опираясь на представление полных пирамидально упорядоченных троичных деревьев в виде массивов, при этом узел в позиции к больше или равен узлам в позициях Зк - I, ЗА; и ЗА; + 1 и меньше или равен узлам в позициях L(A + 1)/ 3j для всех позиций между 1 и N в массиве из элементов. Снижение стоимости, обусловленное меньшей высотой дерева, уравновешивается более высокой стоимостью выбора наибольшего из трех потомков в каждом узле. Подобного рода компромисс зависит от деталей реализации (см. упражнение 9.30). Дальнейшее увеличение количества потомков в каждом узле по всем признакам не дает никакой выгоды.

Рисунок 9.11 иллюстрирует пирамидальную сортировку в действии на файле с произвольной организацией. Поначалу кажется, что этот процесс делает все, что угодно, только не сортировку, поскольку по мере продвижения построения сортирующего

дерева большие элементы перемещаются в начало файла. Однако, в соответствии с ожиданиями, далее метод больше выглядит как зеркальное отображение сортировки выбором. На рис. 9.12 показано, что различные виды данных можно представить в виде сортирующих деревьев, обладающими особыми характеристиками, однако по мере продвижения процесса сортировки к своему завершению все они приобретают вид сортирующего дерева с произвольной организацией.

Естественно, не может не интересовать проблема, какой метод сортировки выбрать для конкретного приложения: пирамидальную сортировку, быструю сортировку или сортировку слиянием. Выбор между пирамидальной сортировкой и сортировкой слиянием сводится к выбору между неустойчивой сортировкой (см. упражнение 9.28) и сортировкой, которая использует дополнительный объем памяти; выбор между пирамидальной сортировкой и быстрой сортировкой сводится к выбору между средним быстродействием сортировки и быстродействием, обеспечиваемым в наихудшем случае. В свое время мы достаточно хорошо потрудились над совершенствованием внутренних циклов быстрой сортировки и сортировки слиянием; решение этих вопросов применительно к сортирующим деревьям мы предоставляем в упражнениях, сопровождающих настоящую главу. Речь отнюдь не идет о повышении производительности пирамидальной сортировки до уровня, превосходящего быструю сортировку, что, собственно говоря, показано посредством эмпирических данных, приведенных в табл. 9.2. Тем не менее, специалисты, изучающие проблему быстрой сортировки на собственных машинах, найдут эти данные поучительными. Как обычно, различные характерные особенности конкретных машин и систем программирования могут сыграть важную роль. Например, быстрая сортировка и сортировка слиянием обладают свойством локальности, которое дает им определенные преимущества на некоторых типах вычислительных машин. Когда операции сравнения становятся недопустимо дорогостоящими, версия Флойда подходит лучше других, поскольку в такого рода ситуациях она становится чуть ли не оптимальной, если принимать во внимание только время выполнения и стоимость используемого пространства памяти.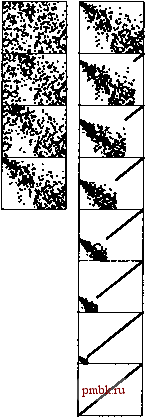

РИСУНОК 9.11. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПИРАМИДАЛЬНОЙ СОРТИРОВКИ На первый взгляд кажется, что процесс построения (слева) нарушает ранее установленный порядок на файле за счет того, что элементы с большими значениями помещаются в начало файла. Затем процесс нисходящей сортировки (справа) начинает действовать как сортировка выбором, при этом сортируемое дерево находится в начальной части файла, а построение отсортированного массива выполняется в конце файла.

РИСУНОК 9.12. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПИРАМИДАЛЬНОЙ СОРТИРОВКИ РАЗЛИЧНЫХ ТИПОВ ФАЙЛОВ.

Время выполнения пирамидальной сортировки не слишком чувствительно к природе входных данных. Независимо от того, какие значения принимают входные величины, наибольший элемент обнаруживается за число шагов, меньшее IgN. На диаграммах показаны: файлы с произвольной организацией, файлы с распределением Гаусса, почти упорядоченные файлы, почти обратно упорядоченные файлы и файлы с произвольной организацией, обладающие 10 различными ключами (вверху, слева направо). Вторая диаграмма сверху демонстрирует сортирующее дерево, построенное с помощью восходящего алгоритма, остальные диаграммы отображают для каждого файла процесс нисходящей сортировки. Вначале сортирующие деревья отображают в какой-то степени исходный файл, но по мере продвижения процесса сортировки они все больше напоминают сортирующие деревья, полученные для файла с произвольной организацией.