9.4. Пирамидальная сортировка

Основную идею, положенную в основу программы 9.6, можно приспособить с таким расчетом, чтобы сортировка массива выполнялась без необходимости использования какого бы то ни было дополнительного пространства памяти. Другими словами, сосредоточившись на задаче сортировки, мы отказываемся от идеи сокрытия очереди по приоритетам, и вместо того чтобы придерживаться ограничений, налагаемых интерфейсом АТД очереди по приоритетам, будем непосредственно применять функции fixUp и fixDown.

Используя программу 9.5 в программе 9.6 непосредственно для перемещения по массиву слева направо, применим функцию fixUp с тем, чтобы элементы, располагающиеся слева от указателя просмотра, образовывали пирамидально упорядоченное полное дерево. Затем, во время выполнения процесса нисходящей сортировки мы помещаем наибольший элемент на то место, которое освобождается по мере уменьшения размеров сортирующего дерева. Иначе говоря, процесс нисходящей сортировки подобен сортировке выбором, однако при этом он пользуется более эффективным методом обнаружения наибольшего элемента в неотсортированной части массива.

Более эффективным, нежели построение сортирующего дерева за счет последовательного выполнения вставок, как показано на рис. 9.5 и 9.6, является построение такого дерева методом прохождения по этому дереву в обратном направлении, формируя поддеревья меньших размеров снизу верх, что иллюстрирует рис. 9.9. Другими словами, мы рассматриваем каждую позицию массива как корень небольшого поддерева и извлекаем пользу из того обстоятельства, что функция fixDown работает на таких сортирующих поддеревьях столь же хорошо, как и на большом дереве. Если оба потомка узла суть сортирующие деревья, то вызов для этого узла функции fixDown приводит к тому, что поддерево с корнем в этом узле также становится сортирующим деревом. Продвигаясь по дереву в обратном направлении и вызывая fixDown в каждом узле, мы по индукции можем восстановить пирамидальный порядок. Просмотр начинается на полпути в обратном направлении вдоль массива, поскольку можно пропустить поддеревья размером 1.

Полная реализация классического алгоритма пирамидальной сортировки (heapsort) представлена в программе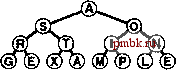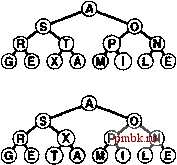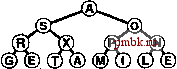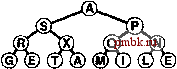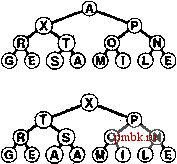

РИСУНОК 9.9. ПОСТРОЕНИЕ СОРТИРУЮЩЕГО ДЕРЕВА СНИЗУ ВВЕРХ

Продвигаясь справа налево и снизу вверх мы строим сортирующее дерево, следя за тем, чтобы поддерево под текущим узлом было пирамидально упорядочено. Общие затраты в наихудшем случае линейно зависимы, поскольку большая часть узлов расположена близко к нижнему уровню дерева.

9.7. И хотя циклы в этой программе на первый взгляд решают совершенно разные задачи (первый выполняет построение сортирующего дерева, второй разрушает это сортирующее дерево для процесса нисходящей сортировки), они построены на основании одной и той же базовой процедуры, которая восстанавливает порядок в дереве, на котором, возможно, уже установлен пирамидальный порядок, за исключением разве что самого корня, используя при этом представление полного дерева в виде массива. На рис. 9.10 показано содержимое массива в примере, соответствующем рис. 9.7-9.9.

Лемма 9.4. Для построения сортирующего дерева снизу вверх требуется линейно зависимое время.

В основе этого утверждения лежит тот факт, что большинство подвергаемых обработке деревьев имеют небольшие размеры. Например, чтобы построить сортирующее дерево из 127 элементов, мы выполняем построение 32 сортирующих деревьев размером 3, 16 деревьев размером 7, 8 деревьев размером 15, 4 деревьев размером 31, двух сортирующих деревьев размером 63 и одного дерева размером 127, так что в худшем случае требуется 32 1 + 16-2 + 8- 3 + 4- 4 + 2- 5 + 1 6 = 120 продвижений (в два раза больше числа операций сравнения). Для n = 2 - I верхняя граница числа продвижений равна

A:2 --=2 - -l<N.

\к<п

Это же доказательство справедливо и в случае, когда Л -ь 1 не является степенью 2.

РИСУНОК 9.10. ПРИМЕР ПИРАМИДАЛЬНОЙ СОРТИРОВКИ

Пирамидальная сортировка представляет собой эффективный алгоритм сортировки, основанный на методе выбора. Сначала строится сортирующее дерево сверху вниз без использования вспомогательной памяти. Верхние восемь строк диаграммы соответствуют рис. 9.9. Далее, из дерева многократно удаляется наибольший элемент. Незаштрихованная часть строк нижней диаграммы соответствуют рис. 9.7и 9.8; заштрихованная часть содержит отсортированный по возрастанию файл.

Эта лемма не имеет особого значения для пирамидальной сортировки, поскольку основная доля времени ее выполнения все еще приходится на N\o$N - время, затрачиваемое на выполнение нисходящей сортировки, однако оно играет важную роль в тех приложениях очередей по приоритетам, в которых операция создать (construct) приводит к алгоритму, обеспечивающему линейную зависимость времени выполнения. Как отмечается на рис. 9.6, построение сортирующего дерева с последовательно выполняемых операций вставить требует в совокупности N\ogN шагов в наихудшем случае (даже если это общее количество шагов оказывается в среднем линейным для файлов с произвольной организацией).

Программа 9.7. Пирамидальная сортировка

Непосредственное применение функции fixDown позволяет построить классический алгоритм пирамидальной сортировки. Цикл for выполняет построение сортирующего дерева; далее, цикл while меняет местами наибольший элемент с последним элементом массива и восстанавливает свойства сортирующего дерева, продолжая этот процесс до тех пор, пока сортирующее дерево не станет пустым. Тот факт, что в условиях представления полного дерева в виде массива указатель pq указывает на а[1-1], позволяет программе рассматривать переданный ей подфайл как первый элемент с индексом 1 (см. рис. 9.2). В некоторых средах программирования это невозможно.

template <class Item>

void heapsort (Item a[ ], int 1, int r) { int k, N = r-1+1; Item *pq = a+1-1; for (k = N/2; к >= 1; к-)

fixDown (pq, k, N) ; while (N>1)

{exch(pq[l], pq[N]);

fixDown (pq, 1, ~N) ; }

Лемма 9.5. Пирамидальная сортировка использует менее 2n\gN сравнений для сортировки N элементов.

Несколько более высокая граница 37Vlg7V следует непосредственно из леммы 9.2. Предложенная здесь граница следует из более точного подсчета на основе леммы 9.4.

Лемма 9.5 и возможность выполнения без использования вспомогательной памяти - вот два основных фактора, которые обусловливают интерес, проявляемый к пирамидальной сортировке на практике, ибо они гарантируют, что сортировка элементов будет выполняться за время, пропорциональное TVlogA независимо от природы входного потока данных. В подобных условиях не бывает входных данных, вызывающих возникновение наихудшего случая, который существенно замедляет выполнение сортировки (в отличие от быстрой сортировки), а пирамидальная сортировка вообще не использует дополнительное пространство памяти (в отличие от сортировки слиянием). Достижение такой гарантированной эффективности для худшего случая требует уплаты своей цены: например, внутренний цикл рассматриваемого алгоритма (стоимость выражается количеством операций сравнения) выполняет больше базовых операций, чем внутренний цикл быстрой сортировки, таким образом, пирамидальная сортировка, по-видимому, работает медленнее быстрой сортировки как на обычных файлах, так и на файлах с произвольной организацией.

Сортирующие деревья можно успешно использовать для решения проблемы выборки к максимальных элементов из N элементов (см. главу 7), особенно в случаях, когда к мало. Мы просто прекращаем выполнение алгоритма пирамидальной сортировки после того, как к элементов будут отобраны из вершины сортирующего дерева.