Базовые процедуры fixUp и fixDown из программ 9.3 и 9.4 позволяют получить прямую реализацию операций изменить приоритет (change priority) и удалить (remove). Для изменения приоритета элемента, находящегося где-то в середине сортирующего дерева, применяется процедура fixUp для перемещения вверх по дереву, если приоритет элемента увеличивается, и процедура fixDown для перемещения вниз по дереву, если приоритет уменьшается. Полная реализация этих процедур применительно к конкретным элементам данных имеет смысл, только если для каждого элемента имеется дескриптор, отслеживающий место этого элемента в структуре данных. Мы подробно рассмотрим реализации, которые выполняют эти действия, в разделах 9.5-9.7.

Лемма 9.3. Операции изменить приоритет (change priority), удалить (remove) и изменить приоритет

(change priority) для АТД очередь по приоритетам могут быть реализованы через сортирующие деревья, такие, что для любой из указанных выше операций требуется выполнение не более чем 2 \%,N операций сравнения на очереди из N элементов.

Поскольку эти операции требуют наличия специальных дескрипторов, отложим рассмотрение реализаций, поддерживающих эти операции, до раздела 9.7 (см. программу 9.12 и рис. 9.14). Все они предусматривают движение по сортирующему дереву вдоль одного пути, возможно, сверху вниз или снизу вверх в худшем случае.

Специально обращаем внимание на тот факт, что в этот список не включена операция объединить Qoin). Эффективное объединение двух очередей по приоритетам, по-видимому, потребует более сложной структуры данных, которая будет подробно рассматриваться в разделе 9.7. С другой стороны, представленный здесь простой метод, в основу которого положен пирамидальный порядок, вполне достаточен для большинства различных приложений. Он использует минимальное дополнительное пространство памяти и обеспечивает высокую эффективность выполнения операций за исключением тех случаев, когда часто и на больших объемах данных выполняются операции объединить.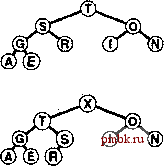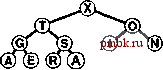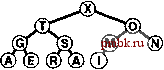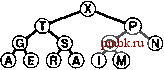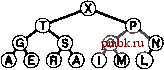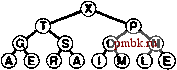

РИСУНОК 9.6. ПОСТРОЕНИЕ СОРТИРУЮЩЕГО ДЕРЕВА СВЕРХУ ВНИЗ (ПРОДОЛЖЕНИЕ)

Представленная последовательность диаграмм отображает процедуру вставки ключей ЕХАМРL Ев сортирующее дерево, построение которого было начато на рис. 9.5. Общая стоимость построения сортирующего дерева размером N составляет Igl + lg2 +...+ IgA, что меньше N\2,N.

Как уже отмечалось выше и как продемонстрировано в программе 9.6, любую очередь по приоритетам можно использовать для построения еще одного метода сортировки. Мы просто вставляем все подлежащие сортировке ключи в очередь по приоритетам, а затем многократно используем операцию удалить наибольший, чтобы удалять их в порядке убывания приоритетов. Такое использования очереди по приоритетам, представленной в виде неупорядоченного списка, соответствует выполнению сортировки выбором, а применение упорядоченного списка соответствует выполнению сортировки вставками.

Программа 9.6. Сортировка с использованием очереди по приоритетам

Чтобы отсортировать подмассив а[1],..., а[г], используя для этой цели АТД очереди по приоритетам, следует при помощи функции insert (вставить) поместить элементы в очередь по приоритетам, а затем с использованием функции getmax (найти наибольший) удалять их в порядке убывания значений приоритетов. Подобный алгоритм сортировки выполняется за время, пропорциональное N\qN, но при этом он требует дополнительного объема памяти, пропорционального количеству сортируемых элементов N (в очереди по приоритетам).

#include PQ.CXX template <class Item> void PQsort(Item a[] , int 1, int r) { int k;

PQ<Item> pq(r-1+1) ;

for (k = 1; к <= r; k++) pq. insert (a [k]) ; for (k = r; к >= 1; к-) а[к] = pq.getmaxO ;

На рис. 9.5 и 9.6. показан пример первой фазы (процесс построения), на которой используется реализация очереди по приоритетам с пирамидальным порядком; на рис. 9.7 и 9.8 представлена вторая фаза (которую будем называть нисходящей сортировкой - sortdown). В условиях практических применений этот метод не выглядит особенно элегантно, поскольку он без особой необходимости копирует сортируемые элементы (в очереди по приоритетам). Действительно, выполнение N последовательных вставок - не самый эффективный способ построения сортирующего дерева, состоящего из N элементов. В следующем разделе при обсуждении реализации классического алгоритма пирамидальной сортировки этим двум вопросам уделяется особое внимание.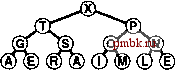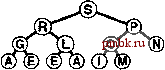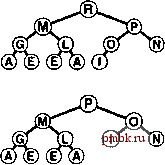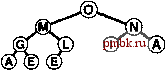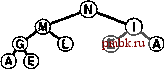

РИСУНОК 9.7. СОРТИРОВКА В СОРТИРУЮЩЕМ ДЕРЕВЕ

После замены наибольшего элемента сортирующего дерева самым правым элементом нижнего уровня можно восстановить пирамидальный порядок за счет перемещения по пути из корня на нижний уровень дерева.

Упражнении

> 9.21, Построить сортирующее дерево, которое получается после того как ключи EASYQUESTIO N вставлены в первоначально пустое сортирующее дерево.

> 9.22. Воспользовавшись соглашением, принятым в упражнении 9.1, представьте последовательность сортирующих деревьев, полученных в результате выполнения операций

PRIO*R**I*T*Y***QUE***U*E

на первоначально пустом сортирующем дереве.

9.23. Поскольку примитив exch используется в операциях по установке пирамидального порядка, элементы загружаются и запоминаются в два раза чаще, чем это необходимо. Предложите более эффективные реализации, которые не сталкиваются с такой проблемой, в духе сортировки вставками.

9.24. Почему мы не пользуемся сигнальной меткой, чтобы избежать проверку j<N в функции fixDown?

о 9.25. Добавить операцию заменить наибольший (replace 4he maximum) в реализацию очереди по приоритетам с пирамидальным порядком в программе 9.5. Рассмотреть случай, когда добавляемое значение больше всех остальных значений в очереди. Совет: К элегантному решению приводит использование элемента pq[0].

9.26. Каким является минимальное количество перемещений ключей, которое потребуется выполнить на сортирующем дереве в операции удалить наибольший (remove maximum)? Приведите пример сортирующего дерева, содержащего 15 элементов, для которого достигается этот минимум.

9.27. Каким является минимальное количество ключей, которое потребуется переместить в процессе выполнения на сортирующем дереве трех последовательных операций удалить наибольший? Приведите пример сортирующего дерева из 15 элементов, для которого достигается этот минимум.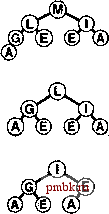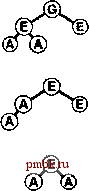

РИСУНОК 9.8. СОРТИРОВКА ИЗ СОРТИРУЮЩЕГО ДЕРЕВА

Представленная здесь последовательность диаграмм отображает удаление остальных ключей из сортирующего дерева на рис. 9.7. Даже если каждый элемент возвращается на нижний уровень, то общие затраты на выполнение этой фазы сортировки не больше \%N+ ...+ Ig2 + Igl, что меньше NlgN.