метода мы перемещаемся вниз по дереву, заменяя ключ заданного узла большим из ключей его потомков до тех пор, пока не достигнем нижнего уровня или точки, в которой нет потомков с большими ключами. В обобщенном виде упомянутые операции применимы не только к бинарным деревьям, но и к любой древовидной структуре. Усовершенствованные алгоритмы, манипулирующие очередями по приоритетам, обычно ориентированы на древовидные структуры общего вида, но в то же время полагаются именно на эти базовые операции, обеспечивающие доступ к наибольшим ключам этой структуры, сосредоточенным в ее верхней части.

Если вообразить себе, что некоторое сортирующее дерево представляет иерархию некой корпорации, в котором каждый потомок представляет подчиненное подразделение (и каждый родитель представляет собой вышестоящее подразделение), то эти операции допускают любопытные аналогии. Восходящий метод соответствуют появлению на сцене нового перспективного управляющего, который продвигается по служебной лестнице с одного поста на другой, более высокий (обмениваясь служебными обязанностями с любым начальником, имеющим более низкую квалификацию) до тех пор, пока этот новый работник не столкнется с более квалифицированным начальником. Нисходящий метод аналогичен ситуации, когда президента некоторой компании сменяет на его посту некто, уступающий ему по квалификации. Если какой-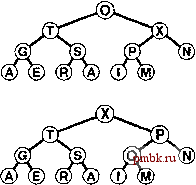

РИСУНОК 9.4. НИСХОДЯЩАЯ УСТАНОВКА СТРУКТУРЫ СОРТИРУЮЩЕГО ДЕРЕВА

Дерево, изображенное в верхней части диаграммы, почти везде пирамидально упорядочено, исключением является корень дерева. Если заменить узел О большим из его потомков (X), то рассматриваемое дерево приобретает пирамидальный порядок, за исключением поддерева с корнем в узле О. Продолжая обмен местами с большим из его двух потомков до тех пор, пока не будет достигнут нижний уровня пирамиды или точка, в которой О больше любого из своих потомков, можно восстановить условие пирамиды на всем дереве. Этой процедурой можно воспользоваться в качестве основы для операции remove the maximum (удалить наибольший) в сортирующем дереве с целью восстановить пирамидальный порядок после замены ключа в корне дерева на ключ, который находится на нижнем уровне в крайней правой позиции.

либо из подчиненных президента, обличенный

наибольшими полномочиями, превосходит по совокупности качеств нового работника, они обмениваются своими обязанностями, и мы двигаемся вниз по служебной лестнице, понижая в должности нового работника и повышая других, пока не будет достигнут уровень компетенции нового работника, когда не остается ни одного подчиненного, превосходящего нового работника по квалификации (этот идеализированный сченарий в реальной жизни встречается редко). Продолжая эту аналогию, движение по сортирующему дереву часто будет называться продвижением.

Программа 9.4. Нисходящая установка структуры сортирующего дерева

Чтобы восстановить пирамидальную структуру в случае, когда приоритет узла понижается, мы двигаемся вниз по сортирующему дереву, меняя при необходимости местами узел в позиции к с большим из его двух потомков, и останавливаемся, когда узел в позиции к не превышает какой-либо из двух своих потомков, или когда

достигнут нижний уровень. Обратите внимание на то обстоятельство, что если N есть четное число и к равно N/2, то узел в позиции к имеет только одного потомка - этот случай требует особого подхода!

Внутренний цикл в этой программе имеет два четко определенных выхода: один для случая, когда достигнут нижний уровень сортирующего дерева, а другой для случая, когда условия сортирующего дерева удовлетворяются где-то внутри дерева. Этот случай может служить прототипным примером необходимости существования конструкции break.

template <class Item>

void fixDown(Item a[ ], int k, int N) {

while (2*k <= N) { int j = 2*k;

if (j < N && a[j] < a[j+l]) if (! (a[k] < a[j])) break; exch (a[k], a[j]); к = j;

Программа 9.5. Очередь по приоритетам на базе сортирующего дерева

Чтобы реализовать операцию вставки, мы увеличиваем N на 1, добавляем новый элемент в конец сортирующего дерева, а затем при помощи функции fixUp восстанавливаем пирамидальный порядок. При выполнении функции getmax (получить наибольший) размер сортирующего дерева должен быть уменьшен на 1, таким образом, мы выбираем в качестве возвращаемого значения величину pq[1], затем уменьшаем размер сортирующего дерева на 1, перемещая значение pq[N] в pq[1], после чего выполняем функцию fixDown с целью восстановить в дереве пирамидальный порядок. Реализации конструктора и функции empty предельно тривиальны. Первая позиция pq[0] массива здесь не используется, но она может быть задействована в качестве сигнальной метки в других реализациях.

template <class Item> class PQ {

private:

Item *pq; Int N; Piiblic:

PQ(int maxN)

{pq = new Item[maxN+l] ; N = 0; } int empty( ) const

{return N==0; } void insert (Item, item)

{pq[++N] = item; fixUp(pq, N;} Item getmax0

exch(pq[l], pq[n] ); fixDown(pq, 1, N-l ); return pq[N-] ;

Как показывает программа 9.5, эти две основные операции позволяют построить эффективную реализацию АТД очереди по приоритетам. Если очередь по приоритетам представлена как пирамидально упорядоченный массив, использование операции

вставить (insert) равносильно добавлению нового элемента в конец массива и перемещение этого элемента по массиву с целью восстановления структуры сортирующего дерева; операция удалить наибольший (remove the maximum) равносильна удалению наибольшего элемента из вершины дерева с последующим размещением элемента, находящегося в конце дерева, в его вершине и перемещением его вниз вдоль массива с целью восстановления структуры сортирующего дерева.

Лемма 9.2. Операции вставить (insert) и удалить наибольший (remove the maximum) для абстрактного типа данных могут быть реализованы на пирамидально упорядоченных деревьях таким образом, что операция вставить требует для своего выполнения на очереди, состоящей из N элементов, не более IgN сравнений, а операция удалить наибольший - не более 2 IgN сравнений.

Обе операции предусматривают перемещение вдоль пути между корнем и нижним уровнем дерева, при этом ни один путь вдоль сортирующего дерева, состоящего из N элементов, не содержит более \gN элементов (см. например, лемму 5.8 и упражнение 5.77). Операция удалить наибольший требует двух сравнений для каждого узла: одну для того, чтобы найти потомка с большим ключом, другую - для того, чтобы принять решение, нужно ли продвигать этого потомка.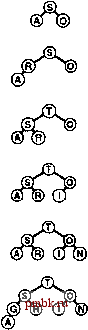

®

На рис. 9.5 и 9.6 показаны примеры, в рамках которых выполняется построение сортирующего дерева путем последовательной вставки элементов в первоначально пустое сортирующее дерево. В представлении сортирующего дерева в виде массива, которое использовалось ранее, этот процесс соответствует пирамидальному упорядочению массива, при этом каждый раз, когда мы переходим к новому элементу, размер сортирующего дерева увеличивается на 1, а для восстановления пирамидального порядка используется функция fisUp. В худшем случае на выполнение этого процесса

требуется время, пропорциональное N\gN (когда каждый новый элемент превосходит по величине все предьщущие, т.е. он проделывает весь путь к корню дерева), но в среднем на это требуется линейное время (новый элемент произвольной природы поднимается всего лишь на несколько уровней). В разделе 9.4 будет рассматриваться способ построения сортирующего дерева (установления в массиве пирамидального порядка) за линейное время в худшем случае.

РИСУНОК 9.5. ПОСТРОЕНИЕ СОРТИРУЮЩЕГО ДЕРЕВА СВЕРХУ ВНИЗ

Представленная последовательность диаграмм описывает операцию вставки ключей AS OR TIN G в первоначально пустое сортирующее дерево. Новые узлы добавляются в сортирующее дерево на нижнем уровне в направлении слева направо. Каждая вставка затрагивает только узлы, которые находятся на пути между точкой вставки и корнем, поэтому затраты в худшем случае пропорциональны логарифму размера сортирующего дерева.