но просто представить полное бинарное дерево в виде массива, поместив корневой узел в позицию 1, его потомков в позицию 2 и 3, узлы следующего уровня в позиции 4, 5, 6, 7 и т.д., как показано на рис. 9.2.

Определение 9.3. Сортирующее дерево есть совокупность узлов с ключами, образующих полное пирамидально упорядоченное бинарное дерево, представленное в виде массива.

Можно было бы воспользоваться связным представлением пирамидально упорядоченных деревьев, но полные деревья предоставляют возможность задействовать компактное представление в виде массива, в котором легко переходить с некоторого узла к его родителю или к его предкам без необходимости поддержки явных связей. Родителя узла, находящегося в позиции /, необходимо искать в позиции и / 2], и, соответственно, два потомка узла в позиции / находятся в позициях 2/ и 2/ + 1. При подобной организации прохождение по такому дереву выполняется проще, чем если бы это дерево было реализовано в связном представлении, поскольку в таком случае могут понадобиться связи дерева, принадлежащие каждому ключу, чтобы иметь возможность перемещаться вверх и вниз по дереву (каждый элемент будет иметь один указатель на родителя и один указатель на каждого потомка). Полные бинарные деревья, представленные в виде массивов, являются жесткими структурами, но все же обладают достаточной гибкостью, чтобы позволить реализовать эффективные алгоритмы, манипулирующие очередями по приоритетам.

В разделе 9.3 мы убедимся в том, что можем воспользоваться сортирующими деревьями для реализации всех операций на очередях по приоритетам (за исключением операции объединить) таким образом, что на свое выполнение они в худшем случае потребуют логарифмическое время. Все такие реализации функционируют вдоль некоторого пути в сортирующем дереве (перемещаясь от родителя к потомкам по направлению вниз или от потомка к родителю по направлению вверх, не меняя при этом направления движения). Как уже было показано в главе 3, все пути в полном дереве, состоящем из Л узлов, содержат в себе порядка XgN узлов: примерно N/2 узлов находятся на самом нижнем уровне, N/A узлов - потомки которых занимают нижний уровень, Л/В узлов - внуки которых занимают нижний уровень и т.д. Каждое следующее поколение узлов содержит наполовину меньше узлов, чем предьщу-щее, всего же может быть максимум IgV поколений.

Можно также воспользоваться явными связными представлениями древовидной структуры для разработки эффективных реализаций операций над очередями по приоритетам. В качестве примеров рассматриваются полные деревья с тремя связями (см. раздел 9.5), сортировка повторной выборкой (см программу 5.19) и биномиальные очереди (см. раздел 9.7). Как и в случае простых стеков и очередей, одна из главных причин, побуждающих рассматривать связные представления, заключается в том, что они освобождают от необходимости заранее знать максимальные размеры очереди, что требуется в обязательном порядке в случае представления в виде массива. Мы также можем извлечь в некоторых ситуациях определенную пользу из гибкости, обеспечиваемой связными структурами, при разработке эффективных алгоритмов. Читателям, которые не имеют достаточного опыта использования явных древовидных структур, мы настоятельно рекомендуем прочитать главу 12, чтобы изучить базовые методы реализации даже более важных абстрактных типов данных, таких как сим-

вольные таблицы, прежде чем иметь дело со связными представлениями деревьев, рассматриваемых в упражнениях этой главы и в разделе 9.7. Однако внимательное изучение связных структур можно оставить до второго чтения, поскольку основной темой настоящей главы является сортирующее дерево (представление в виде массива без связей полного пирамидально упорядоченного дерева).

Упражнения

> 9.17. Является ли массив, отсортированный в нисходящем порядке, сортирующим деревом?

о 9.18. Наибольший элемент сортирующего дерева должен появиться в позиции 1, а второй наибольший элемент должен занимать позицию 2 или 3. Представьте список позиций в сортирующем дереве из 15 элементов, в котором к-й наибольший элемент (i) может появиться и (ii) не может появиться, для А: = 2, 3, 4 (в предположении, что все значения попарно различны).

9.19. Решить задачу 9.18 для общего значения к как функции от Л, представляющего собой размер сортирующего дерева.

9.20. Решить задачи 9.18 и 9.19 для А:-го наименьшего элемента.

9.3. Алгоритмы для сортирующих деревьев

Все алгоритмы очередей по приоритетам для сортирующих деревьев работают таким образом, что сначала вносят простое изменение, способное нарушить структуру пирамиды, затем выполняют проход вдоль пирамиды, внося при этом в сортирующее дерево такие изменения, которые гарантируют, что структура сортирующего дерева сохраняется везде. Этот процесс иногда называют установлением пирамидального порядка (heapifying). Возможны два случая. Когда приоритет какого-либо узла увеличивается (или в нижний уровень сортирующего дерева добавляется новый узел), мы должны двигаться вверх по дереву, чтобы восстановить структуру сортирующего дерева. Когда приоритеты каких-либо узлов уменьшаются (например, при замене корневого узла новым узлом), необходимо пройти вниз по дереву, чтобы восстановить структуру сортирующего дерева. Для начала обсудим, как реализовать две эти базовые функции, а затем подумаем, как их использовать в различных операциях с очередями по приоритетам.

Если свойства сортирующего дерева нарушены из-за того, что ключ некоторого узла становится больше ключа родительского узла, можно сделать шаг в направлении исправления этого нарушения, обменяв местами этот узел с его родителем. После обмена этот узел становится больше, чем оба его потомка (один из них - это прежний родитель, другой меньше, чем старый родитель, поскольку он был потомком этого узла), но все еще может оставаться больше своего родителя. Мы можем устранить и это нарушение аналогичным способом и продвигаться далее вверх по дереву, пока не достигнем узла с наибольшим ключом, каковым является корень дерева. Пример описанного процесса показан на рис. 9.3. Программа проста и понятна, в ее основе лежит тот факт, что родитель узла, занимающего позицию к в сортирующем дереве, находится в позиции к / 2 этого дерева. Программа 9.3 представляет собой реализацию функции, которая восстанавливает возможные нарушения, обусловленные

увеличением приоритета в заданном узле сортирующего дерева, благодаря продвижению вверх по дереву.

Программа 9.3. Восходящая установка структуры сортирующего дерева

Чтобы восстановить пирамидальную структуру после того, как приоритет одного из узлов сортирующего дерева изменился, мы продвигаемся вверх по дереву, меняя при необходимости местами узел в позиции к с его родителем (который находится в позиции к/2) и продолжаем этот процесс до тех пор, пока выполняется условие а[к/2] < а[к] или пока не выйдем в вершину сортирующего дерева.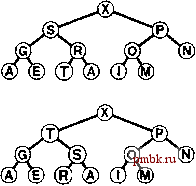

template <class Item> void fixUp(Item a[], int k) {

while (k > 1 && a[k/2] < a[k]) { exch (a[k], a[k/2]); к = k/2; }

Если свойство пирамидальности сортирующего дерева было нарущено в силу того, что ключ какого-либо узла становится меньше, чем один или оба ключа его потомков, выполняются шаги с целью устранения нарущения путем замены узла на больший из его двух потомков. Такая замена может вызвать нарушение свойств сортирующего дерева на узле-потомке; это нарушение устраняется аналогичным путем и выполняется продвижение вниз по дереву до тех пор, пока не будет достигнут узел, оба потомка которого меньше его самого, либо нижний уровень дерева. Пример процесса показан на рис. 9.4. Опять-таки, программный код учитывает то обстоятельство, что потомки узла сортирующего дерева в позиции к занимают в нем позиции 2к и 2к+1.

Профамма 9.4 содержит реализацию функции, которая восстанавливает сортирующее дерево после возможных нарушений по причине повышения приоритета заданного узла, перемещаясь вниз по этому дереву. Эта функция должна знать размер сортирующего дерева (N), чтобы иметь возможность отследить момент, когда будет достигнут нижний уровень дерева.

Обе эти операции не зависят от способа представления структуры дерева, если возможен доступ к родителям (восходящий метод) и к потомкам (нисходящий метод) любого узла. В случае восходящего метода мы перемещаемся вверх по дереву, заменяя ключ заданного узла ключом его родителя до тех пор, пока не выйдем на корневой узел или на родителя с большим (или равным) ключом. В случае нисходящего

РИСУНОК 9.3. ВОСХОДЯЩАЯ УСТАНОВКА СТРУКТУРЫ СОРТИРУЮЩЕГО ДЕРЕВА

Иа верхнем дереве, показанном на диаграмме, установлен пирамидальный порядок, в который не вписывается узел Тна нижнем уровне. Если мы поменяем Тместами с его родителем, дерево остается пирамидально упорядоченным, за исключением разве что того случая, когда Т оказывается больше своего нового родителя. Продолжая обмен местами узла Тсо своими родителями до тех пор, пока мы не выйдем на своем пути на корневой узел, либо на узел, который больше Т, мы можем установить пирамидальный порядок во всем дереве. Мы можем использовать эту процедуру в качестве основы для операции insert (вставить), выполняемой на сортирующих деревьях с целью восстановления пирамидального порядка после добавления в это дерево нового элемента (крайнюю правую позицию на нижнем уровне, вводя в дереве при необходимости новый уровень).