Таблица 9.1. Стоимость операций, поддерживающих очередь по приоритетам, для наихудшего случая

Показатели производительности реализации АТД очереди по приоритетам колеблются в широких пределах, что следует из данной таблицы, содержащей временные показатели для наихудшего случая (в пределах постоянного множителя для больших N) в условиях различных методов. Элементарные методы (первые четыре строки) требуют для выполнения некоторых операций постоянного времени и линейного времени для остальных; более совершенные методы гарантируют постоянное или линейное время выполнения для большего числа или даже для всех операций.

Удалить Найти Изменить

Вставить наибольший Удалить наибольший приоритет Объединить

упорядоченный массив N 1 Л/ 1 N N

упорядоченный список Л/ 1 1 1 N N

неупорядоченный массив 1 Л/ 1 Л/ 1 N

неупорядоченный список 1 Л/ 1 Л/ 1 1

сортирующее дерево 1дЛ/ 1дЛ/ 1дЛ/ 1 1дЛ/ N

биномиальная очередь 1дЛ/ 1дЛ/ 1дЛ/ \дМ \дМ \gN

теоретически наилучший 1 1дЛ/ 1дЛ/ 1 1 1

Для наихудшего случая в условиях различных реализаций показатели стоимости различных операций (пределах постоянного коэффициента) для очереди по приоритетам размера N сведены в таблицу 9.1.

При разработке завершенной реализации необходимо соблюдать все интерфейсные требования - в особенности то, как клиентские профаммы осуществляют доступ к узлам при выполнения операций удалить и изменить приоритет, и как они осуществляют доступ к самим очередям по приоритетам как к типам данных при выполнении операции объединить. Эти проблемы изучаются разделах 9.4 и 9.7, в которых рассматриваются две завершенных реализации: в одной реализации используются двухсвязные неупорядоченные списки, а в другой - биномиальные очереди.

Время выполнения клиентской профаммы, использующей очереди по приоритетам, зависит не только от ключей, но также и от смеси различных операций. Не следует упускать из виду простые реализации, поскольку во многих практических ситуациях они довольно часто оказываются эффективнее более сложных методов. Например, реализация, работающая с неупорядоченными списками, может оказаться приемлемой в приложениях, в которых выполняются лишь немногие операции удалить наибольший и в то же время очень большое количество вставок, тогда как упорядоченный список лучше подходит в тех случаях, когда выполняется большое число операций найти наибольший либо когда вставляемые элементы преимущественно больше уже находящихся в очереди по приоритетам.

Упражнения

> 9.5. Найти недостатки следующей идеи: почему бы для реализации операции найти наибольший (find the maximum) не отслеживать максимальное значение из числа элементов, включенных на текущий момент, а затем возвращать это значение как результат операции?

t> 9.6. Показать содержимое массива после выполнения последовательности операций из рис. 9.1.

9.7. Напишите реализацию основного интерфейса очереди по приоритетам, который использует упорядоченный массив в качестве базовой структуры данных.

9.8. Напишите программную реализацию основного интерфейса очереди по приоритетам, которая использует неупорядоченный связный список в качестве базовой структуры данных Совет: см. программу 4.8 и 4.14.

9.9. Напишите профаммную реализацию основного интерфейса очереди по приоритетам, который использует упорядоченный связный список в качестве базовой структуры данных Совет: см. профамму 3.11.

о 9.10. Рассмотреть ленивую реализацию, в условиях которой список упорядочивается только когда выполняются операции удалить наибольший или найти наибольший. Вставки, сделанные с момента предыдущей сортировки, содержатся в отдельном списке, затем они сортируются и при необходимости подвергаются слиянию. Рассмотреть преимущества такой реализации перед элементарными реализациями, в основу которых положены неупорядоченные и упорядоченные списки.

9.11. Написать клиентскую программу-драйвер, которая использует функцию insert для заполнения очереди по приоритетам, затем функцию getmax для удаления половины ключей, затем снова insert для заполнения очереди, после чего для удаления всех ключей используется getmax, и все это проделывается многократно над случайными последовательностями ключей различной длины, изменяющейся в широких пределах. Кроме того, программа должна измерять время, затраченное на каждое выполнение программы, и распечатывать или строить графики среднего времени выполнения.

9.12. Написать клиентскую профамму, представляющую собой драйвер производительности, которая использует функцию insert для заполнения очереди по приоритетам, затем выполняет функции getmax и insert столько раз, сколько она способна их выполнить в течение 1 секунды на случайных последовательностях ключей разной длины, значения которой колеблются в широких пределах, от малых до больших. Программа должна измерять время, затраченное на каждое выполнение программы, и распечатывать или строить графики среднего числа функций getmax, которое удалось выполнить.

9.13. Воспользуйтесь клиентской программой из упражнения 9.12, чтобы сравнить реализацию неупорядоченного массива, представленную программой 9.2, с реализацией неупорядоченного списка из упражнения 9.8.

9.14. Воспользуйтесь клиентской программой из упражнения 9.12, чтобы сравнить реализацию упорядоченного массива с реализацией упорядоченного списка из упражнений 9.7 и 9.9.

9.15. Написать клиентскую программу-драйвер, которая использует функции интерфейса очереди по приоритетам из программы 9.1 в трудных и патологических случаях, которые могут встретиться в практических реализациях. В категорию простых случаев входят уже упорядоченные ключи, ключи, установленные в обратном порядке, случаи, когда все ключи одинаковы и когда последовательности ключей содержат только два различных значения.

9.16. (За этим упражнением на самом деле стоят 24 упражнения.) Докажите правильность границ, установленных для 4 элементарных реализаций, представленных в таблице 9.1, используя для доказательства реализацию операций вставить (insert) и удалить наибольший (remove the maximum) из профаммы 9.2, и реализации, выполненные в упражнениях 9.7-9.9, а также формальное описание методов реализации других операций. Что касается операций удалить (remove), изменить приоритет (change priority) и объединить Qoin), предположите, что имеется средство, обеспечивающее прямой доступ к объекту ссылки.

9.2. Пирамидальная аруктура данных

Основной темой настоящей главы является простая сфуктура данных, получившая название сортирующего дерева (heap), которая может эффективно поддерживать основные операции в очереди по приоритетам. В сортирующем дереве записи хранятся в виде массива таким образом, что каждый ключ обязательно принимает значение большее, чем значения двух других ключей, занимающих относительно него строго определенные положения. В свою очередь, каждый из этих ключей должен быть больше, чем два других определенных ключа и т.д. Подобное упорядочение легко обнаружить, если рассматривать эти ключи как входящие в бинарную древовидную структуру с ребрами, идущими от каждого ключа к двум другим ключам, о которых известно, что они меньше его по значению.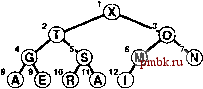

1 2 3 4 5 6 7 X Т О G S М N

9 1011 12 Е R А I

Определение 9.2. Дерево называется пирами-дольно упорядоченным (heap-ordered), если ключ в каждом его узле больше или равен ключам всех потомков этого узла (если таковые имеются). Эквивалентная формулировка: ключ в каждом узле пирамидально упорядоченного дерева меньше или равен ключу узла, который является родителем данного узла.

Лемма 9.1. Ни один из узлов пирамидально упорядоченного дерева не может иметь ключа, большего чем ключ корня дерева.

На любое дерево можно наложить ограничения, обусловленные пирамидальной упорядоченностью. Однако особенно удобно пользоваться полным бинарным деревом (complete binary tree). Из главы 3 известно, что мы можем начертить такую сфуктуру, поместив в верхней части страницы корневой узел, а затем спускаясь вниз по странице и перемещаясь слева направо, подсоединять к каждому конкретному узлу предыдущего уровня два узла текущего уровня до тех пор, пока не будут помещены все N узлов. Достаточ-

РИСУНОК 9.2. ПРЕДСТАВЛЕНИЕ ПОЛНОГО ДВОИЧНОГО ДЕРЕВА В ВИДЕ ПИРАМИДАЛЬНО УПОРЯДОЧЕННОГО МАССИВА

Если рассматривать элемент в позиции j/2J массива как родителя элемента в позиции i, д.1я 2 < i < IV (или, что эквива.1ентно, считая i-u элемент родителем 21-го и 2/+1 -го элементов), то становится возможным удобное представление совокупности элементов массива в виде дерева. Такое соответствие эквивалентно нумерации полного двоичного дерева (элементы на нижнем уровне нумеруются, начиная с самого левого) по уровням. Дерево называется пирамидально упорядоченным, если ключ любого заданного узла больше или равен ключам узлов потомков. Сортируюиее дерево есть представление в виде массива полного упорядоченного двоичного дерева, /-и элемент сортирующего дерева больше или равен по величине 2/-го и 2/+I -го элементов.