обратным порядком: любое прохождение дерева, во время которого обход поддерева, принадлежащего конкретному узлу, должен быть завершен перед посещением самого узла, дает правильный алгоритм. Единственное ограничение заключается в том, что сливаемые файлы должны быть сначала отсортированы. Что касается сортировки слиянием, то удобно сначала выполнять все слияния типа 1-c-l, затем все слияния типа 2-С-2, затем типа 4-с-4 и так далее. Такая последовательность соответствует обходу дерева по уровням, постепенно поднимаясь по дереву снизу вверх.

Программа 8.5. Восходящая сортировка слиянием

Восходящая сортировка слиянием состоит из последовательности проходов по всему файлу с выполнением слияний вида m-c-m, при этом m на каждом проходе удваивается, так что в заключение производится слияние типа т-с-х для некоторого х, меньшего или равного т.

inline int min (int A, int B) { return (A < B) ? A : B; } template <class Item>

void mergesortBU(Item a[] , int 1, int r)

for (int m is 1; m <= r-l; m = m+m) for (int i = 1; i <= r-m; i += m+m) merge (a, i, i+m-1, min(i+m+m-l, r)) ;

asort i ngexample a s

i t

a 0 r s

g i n t

a e m x

e l p

a g i n о r s t

a e e l m p x aaeegi lmnoprstx

РИСУНОК 8.4. ПРИМЕР ВОСХОДЯЩЕЙ СОРТИРОВКИ СЛИЯНИЕМ

Каждая строка диаграммы показывает результат вызова функции в процессе восходящей сортировки слиянием. Слияния вида 1-с-1 выполняются первыми: слияние А и S дает AS; затем производится слияние О и R, в результате получаем OR и так далее. Поскольку длина файла является нечетной величиной, последнее Е в слиянии не участвует. На втором проходе выполняются слияния типа 2-С-2: AS сливается с OR, в результате получает AORS и т.д. Сортировка файла завершается слиянием вида 4-С-4, 4-с-З и, наконец, 8-С-7.

В главе 5 на нескольких примерах можно бьшо заметить, что когда мы рассуждаем в направлении снизу вверх, имеет смысл переориентировать мышление в направлении стратегии объединяй и властвуй , в рамках которой принимаются решения относительно малых подзадач, которые объединяются для получения решения более крупной задачи. В частности, нерекурсивный вариант сортировки слиянием в профамме 8.5 получается следующим образом: все элементы файла рассматриваются как упорядоченные подсписки длиной 1. Затем мы просматриваем этот список, выполняя слияния вида l-c-l, что дает упорядоченные подсписки размером 2, затем мы просматриваем полученный список, выполняя при этом слияния вида 2-С-2, что даст упорядоченный подсписок размером 8, и так далее до тех пор, пока весь список не станет упорядоченным. Завершающий подсписок не всегда может оказаться того же размера, что и все другие, если размер файла не является степенью 2, тем не менее, можно слить и его.

Если размер файла является степенью 2, то множество слияний, выполняемых восходящей сортировкой слиянием, в точности совпадает со слияниями, выполняемыми рекурсивной сортировкой слиянием, однако последовательность слияний будет другой.

Восходящая сортировка слиянием соответствует прохождению дерева типа разделяй и властвуй в порядке уровней, снизу вверх. В противоположность этому, мы обращались к рекурсивному алгоритму как к нисходящей сортировке слиянием, поскольку при обратном порядке прохождения дерева просмотр начинается сверху и следует вниз по дереву.

Если размер файла не может быть представлен степенью 2, восходящий алгоритм дает другое множество слияний, как показано на рис. 8.5. Восходящий алгоритм соответствует дереву, построенному по принципу объединяй и властвуй (см. упражнение 5.75), который отличается от дерева типа разделяй и властвуй , относящемуся к категории нисходящих алгоритмов. Однако вполне можно устроить так, чтобы последовательность слияний, порожденных рекурсивным методом, была такой же, как и аналогичная последовательность, полученная в рамках нерекурсивного метода, тем не менее, нет особых причин делать это, поскольку разница в затратах на их реализацию по отнощению к общим затратам незначительная.

Леммы 8.1-8.4 справедливы и для восходящей сортировки слиянием, при этом имеют место следующие дополнительные леммы:

Лемма 8.5. Все слияния на каждом проходе восходящей сортировки слиянием манипулируют файлами, размер которых выражен степенью 2, за исключением разве что размера последнего файла.

Это факт легко установить методом индукции.

Лемма 8.6. Количество проходов при восходящей сортировке слиянием по файлу из N элементов в точности равно числу бит в двоичном представлении N (при этом ведущие нули игнорируются).

На каждом проходе восходящей сортировки слиянием размер упорядоченных подфайлов удваивается, так что размер подсписков после к проходов составит 2 Таким образом, количество проходов, необходимое для сортировки файла из N элементов, есть наименьшее к такое, что 2* > N, точной величиной к является UgNl, т.е. количество бит в двоичном представлении N. Это можно доказать методом индукции или путем анализа структурных свойств деревьев типа объединяй и властвуй .

РИСУНОК 8.5. РАЗМЕРЫ ФАЙЛОВ ПРИ ВОСХОДЯЩЕЙ СОРТИРОВКЕ СЛИЯНИЕМ

Схемы восходящей сортировки слиянием кардинально отличаются от схем, применяемым при нисходящей сортировке слиянием (рис. 8.3), когда размер файла не является степенью 2. Что касается восходящей сортировки слиянием, то все размеры подфайлов, исключая, возможно, последний, являются степенью 2. Эти различия представляют интерес для понимания базовых структур алгоритмов, однако на производительности сортировки они отражаются лишь незначительно.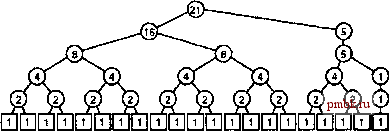

РИСУНОК 8.6. ВОСХОДЯЩАЯ СОРТИРОВКА СЛИЯНИЕМ

Нам потребуется всего лишь семь проходов, чтобы отсортировать 200 элементов, применяя для этой цели восходящую сортировку слиянием. На каждом проходе количество отсортированных подфайлов уменьшается вдвое, зато их длина удваивается (за исключением разве что последнего подфайла).

Ш/ ш

Процесс выполнения восходящей сортировки слиянием показан на рис. 8.6. Сортировка 1 миллиона элементов выполняется за 20 проходов по данным, 1 миллиарда за 30 проходов и т.д.

Кратко подводя итоги, отметим, что нисходящие и восходящие сортировки суть два достаточно простых алгоритма, в основу которых положена операция слияния двух упорядоченных подфайлов в результирующий объединенный упорядоченный файл. Оба алгоритма тесно связаны между собой и даже выполняют одно и то же множество слияний, если размер исходного файла является степенью 2, но они отнюдь не идентичны. Рисунок 8.7 демонстрирует различия динамических характеристик алгоритмов на примере большого файла. Каждый алгоритм может использоваться на практике, если речь не идет об экономии пространства памяти и желательно обеспечить гарантированное время выполнения для наихудшего случая. Оба алгоритма представляют интерес как прототипы более универсальных алгоритмов типа разделяй и властвуй и объединяй и властвуй .

Упражнения

8.24. Показать, какие слияния выполняет нисходящая сортировка слиянием (профамма 8.5) на ключах EASYQUESTION.

8.25. Реализовать восходящую сортировку слиянием, которая начинает с того, что сортирует блоки по М элементов каждый методом вставок. Определить эмпирическим путем значение М, для которого разработанная программа выполняется быстрее всего при сортировке файлов с произвольной организацией, содержащих N элементов при Л= 10 10\ 10 и 10

8.26. Нарисовать деревья, которые отображают слияния, выполняемые программой 8.5 для 7V- 16, 24, 31, 32, 33 и 39.

8.27. Написать программу рекурсивной сортировки слиянием, которая выполняет те же слияния, что и восходящая сортировка слиянием.

8.28. Написать программу восходящей сортировки слиянием, которая выполняет те же слияния, что и нисходящая сортировка слиянием. (Это упражнение намного труднее, чем упражнение 8.27).