тода (время ее выполнения пропорционально N\ogN), который допускает возможность реализации, обладающей устойчивостью. Эти утверждения сравнительно нетрудно доказать.

Как было показано в главе 5 (и для быстрой сортировки в главе 7), можно воспользоваться древовидной структурой, чтобы получить наглядное представление о структуре рекурсивных вызовов рекурсивного алгоритма, что поможет понять все варианты рассматриваемого алгоритма и провести его анализ. Что касается сортировки слиянием, то структура рекурсивных вызовов целиком зависит от размеров ввода. Для любого заданного Л мы строим дерево, получивщее название дерево разделяй и властвуй , которое описывает размер подфайлов, подвергаемых обработке в процессе выполнения профаммы 8.3 (см. упражнение 5.73): если N есть 1, то в таком дереве имеется всего лищь один узел с меткой 1; в противном случае дерево состоит из узла, содержащего файл размером N, представляющего корень, поддерева, представляющего левый подфайл размера L-/V/2J и поддерева, представляющего правый подфайл размера \N / 2]. Следовательно, каждый узел этого дерева соответствует вызову функции mergesort, при этом метка дает представление о размере задачи, соответствующей конкретному рекурсивному вызову. Если Л есть степень 2, то такая конструкция приводит к получению полностью сбалансированного дерева со степенью 2 во всех узлах и 1 во всех внешних узлах. Когда N не является степенью 2, сложность дерева увеличивается. Примеры обоих вышеуказанных случаев иллюстрируются диаграммой на рис. 8.3. Мы сталкивались с подобного рода деревьями раньше, в разделе 5.2, когда изучали алгоритм со структурой рекурсивных вызовов, аналогичной применяемой в сортировке слиянием.

Программа 8.3. Нисходящая сортировка слиянием

Эта базовая реализация сортировки слиянием является примером рекурсивной программы, прототипом которой служит принцип разделяй и властвуй . Она выполняет сортировку массива all],..., а[г] путем деления его на две части а[1],...,а[т] и a[m+1],...,a[r] с последующей их сортировкой независимо друг от друга (через рекурсивные вызовы) и слияния полученных упорядоченных подфайлов с тем, чтобы в конечном итоге получить отсортированный исходный файл. Функция может потребовать использования вспомогательного файла, достаточно большого, чтобы принять копию входного файла, однако эту абстрактную операцию удобно рассматривать как обменное слияние (см. текст).

template <class Item>

void mergesort (Item a[], int 1, int r) {if (r <= 1) return; int m = (r+l)/2; mergesort(a, 1, m) ; mergesort(a, m+1, r) ; merge(a, i, m, r) ;

Структурные свойства сбалансированных деревьев, построенных по принципу разделяй и властвуй , имеют непосредственное отношение к анализу сортировки слиянием. Например, общее количество операций сравнения, выполняемых алгоритмом, в точности равно сумме всех меток узлов.

I ill I ill I illt Л11 ill I ill I lit I ill I ill I ill I ill I ill I ill I ill I ill I ill I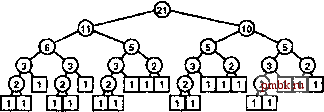

РИСУНОК 8.3. ДЕРЕВЬЯ, ПОСТРОЕННЫЕ ПО ПРИНЦИПУ РАЗДЕЛЯЙ И ВЛАСТВУЙ

Эти три диаграммы иллюстрируют размеры подзадач, возникающих в процессе выполнения нисходящей сортировки слиянием. В отличие от деревьев, соответствующих, например, быстрой сортировке, эти схемы определяются только размерами исходного файла, а не значениями ключей, присутствующих в файле. Верхняя диаграмма показывает, как сортируется файл, состоящий их 32 элементов. Мы (рекурсивно) сортируем два файла по 16 элементов, затем выполняем их слияние. Файлы сортируются по 16 элементов с выполнением (рекурсивной) сортировки файлов по 8 элементов и т.д. Для файлов, размер которых нельзя представить в виде степени 2, схема оказывается несколько более сложной, в чем нетрудно убедиться из нижней диаграммы.

Лемма 8Л. Сортировка слиянием требует выполнения примерно NlgN операций сравнения для сортировки любого файла из N элементов.

В реализациях, описанных в разделах 8.1 и 8.2, каждое слияние типа (N/2) на (ЛУ2) требует сравнений (это значение будет для разных файлов отличаться на 1 или на 2, в зависимости от того, как используются служебные метки). Следовательно, общее количество сравнений при сортировке в полном объеме может быть описано стандартным сбалансированным рекуррентным соотношением: Млг= Л/[л/2] + Л/[л,/21 + N, где М\=0. Такое рекуррентное соотношение описывает также сумму меток узлов и длину внешнего пути дерева типа разделяй и властвуй с N узлами (см. упражнение 5.73). Это утверждение нетрудно проверить, когда является степенью числа 2 (см. формулу 2.4) и доказать методом индукции для произвольного Л. Упражнения 8.12-8.14 содержат непосредственное доказательство.

Лемма 8.2. Сортировка слиянием использует дополнительное пространство, пропорциональное N.

Это факт непосредственно следует из обсуждения, приведенного в разделе 8.2. Мы можем предпринять некоторые шаги, Мабы уменьшить размеры используемого дополнительного пространства за счет существенного усложнения алгоритма (см., например, упражнение 8.21). Как будет показано в разделе 8.7, сортировка слиянием также эффективна, если сортируемый файл организован как связный список, В этом случае указанное свойство сохраняется, однако для связей расходуется дополнительное пространство памяти. В случае массивов, как отмечалось в разделе 8.2, можно выполнять обменное слияние (обсуждение этой темы будет продолжено в разделе 8.4), однако эта стратегия вряд ли оправдывается на практике.

Лемма 8.3. Сортировка слиянием устойчива, если устойчив используемый при этом метод слияния.

Это утверждение легко проверить методом индукции. Для реализации метода слияния, предложенного в программе 8.1, легко показать, что относительная позиция дублированных ключей не нарушается. Однако, чем сложнее алгоритм, тем выше вероятность того, что эта устойчивость будет нарушена (см. упражнение 8.6).

Лемма 8.4. Потребность ресурсов со стороны сортировки слиянием не чувствительна по отношению к исходному порядку входного файла.

В наших реализациях входные данные определяют разве что порядок, в котором элементы обрабатываются во время слияний. Каждый проход требует пространства памяти и числа шагов, пропорциональных размеру подфайла, что обусловливается необходимостью затрат на перемещение данных во вспомогательный файл. Соответствующие две ветви оператора if могут потребовать слегка отличающихся значений времени для выполнения компиляции, что в свою очередь приводит к некоторой зависимости времени выполнения от характера входных данных, однако число сравнений и других операций не зависит от того, как упорядочен входной файл. Обратите внимание на то, что это отнюдь не эквивалентно утверждению, что алгоритм не адаптивный (см. раздел 6.1) - последовательность сравнений не зависит от упорядоченности входных данных.

Упражнения

> 8.9. Показать, что слияние, реализуемое программой 8.3, не сортирует ключи EASYQUESTION.

8.10. Начертить деревья типа разделяй и властвуй для N = 16, 24, 31, 32, 33 и 39.

8.11. Реализовать рекурсивную сортировку слиянием для массивов, воспользовавшись идеей трехпутевой, а не двухпутевой сортировки.

о 8.12. Доказать, что все узлы с метками 1 в деревьях типа разделяй и властвуй , расположены на двух нижних уровнях.

о 8.13. Доказать, что метки в узлах на каждом уровне сбалансированного дерева размером /V, в сумме дают 7V, за исключением, возможно, нижнего уровня.

о 8.14. Используя упражнения 8.12 и 8.13, доказать, что количество сравнений, необходимых для выполнения сортировки слиянием, находятся в пределах между NlgNu N\gN + N.

8.15. Найти и доказать зависимость между числом сравнений, используемых сортировкой слиянием, и количеством бит в rig/vl-разрядных положительных числах, меньших N.