7.19. Выполните эмпирические исследования с целью определения среднего размера стека, используемого базовым рекурсивным алгоритмом для сортировки файла с произвольной организацией, состоящего из Лэлементов, причем Л= Ю, 10 10и 10

7.20. Найти среднее число подфайлов размера О, 1 и 2, когда быстрая сортировка используется для сортировки произвольно организованного файла из Л элементов.

7.4. Подфайлы небольших размеров

Заметное повыщение эффективности быстрой сортировки следует из того факта, что рекурсивная программа гарантировано вызывает сама себя для работы со множеством подфайлов небольших размеров. Следовательно, когда она сталкивается с подфайлами небольших размеров, она обязана использовать по возможности самый лучший метод работы с ними. Один из очевидных способов достижения данной цели предусматривает соответствующую проверку в начале рекурсивной программы на участке от оператора return до вызова сортировки методом вставки, например,

if (г-1 <= М) insertion(a, 1, г);

Здесь М - это некоторый параметр, точное значение которого зависит от реализации. Мы можем определить наилучшее значение М путем анализа либо эмпирических исследований. Обычно в результате подобных исследований выясняется, что время выполнения мало меняется, если М принимает значения в диапазоне примерно от 5 до 25, при этом значение времени выполнения, когда М попадает в этот диапазон, отличается от значения этого показателя при естественном выборе М=\ не более, чем на 10 процентов (см. рис.7.8).

Несколько более простой и чуть более эффективный по сравнению с сортировкой вставками способ обращения с подфайлами небольших размеров по мере их появления состоит в том, чтобы поменять проверку в начале программы на

if (r-l <= М) return;

Другими словами, в процессе разделения небольшие подфайлы просто игнорируются. В условиях нерекурсивной реализации это можно сделать, отказавшись от помещения в стек любых файлов с размерами меньшими М, либо игнорируя все файлы с размерами меньшими М, которые будут обнаруживаться в стеке. По окончании операции разделения получается практически отсортированный файл. При этом, как уже отмечалось в разделе 6.5, метод вставок является наилучшим методом сортировки подобного рода файлов. То есть, сортировка вставками работает с таким файлом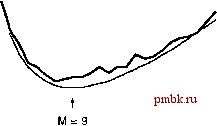

РИСУНОК 7.8. ОТСЕЧЕНИЕ ФАЙЛОВ МАЛЫХ РАЗМЕРОВ

Выбор оптимального значения размера в целях отсечения небольших файлов приводит к уменьшению среднего времени выполнения сортировки на 10 процентов. Выбор точного значения не критичен; значения этого показателя в достаточно широких пределах (приблизительно от 5 до 20) дает практически одинаково хорошие результаты для большей части приложений. Жирная ломаная линия (сверху) получена эмпирическим путем; тонкая линия (снизу) была рассчитана аналитически.

почти так же хорошо, как и с совокупностью файлов небольших размеров, когда они подвергаются сортировке вставками непосредственно. При использовании данного метода следует соблюдать осторожность, ибо сортировка вставками скорее всего будет работать, даже если алгоритм быстрой сортировки содержит фатальную ошибку, из-за которой эта сортировка просто функционировать не будет. Только резкое возрастание затрат ресурсов может служить сигналом о том, что что-то не в порядке.

Рисунок 7.9 иллюстрирует этот процесс на примере крупного файла. Даже при сравнительно радикальном отсечении файлов небольших размеров та часть программы, которая выполняет быструю сортировку, выполняется быстро, поскольку в процесс разделения вовлечено относительно небольшое количество элементов. Сортировка вставками, завершающая выполнение программы, также выполняется быстро, поскольку на обработку ей передается почти упорядоченный файл.

Этот метод с большой пользой можно применять всякий раз, когда мы имеем дело с рекурсивным алгоритмом. В силу особенностей рекурсивных алгоритмов можно быть уверенным в том, что все они основную часть своего времени будут заняты решением небольших задач; в любом случае для работы с небольшими файлами в нашем распоряжении имеются алгоритмы решения в лоб с низкими непроизводительными затратами. Благодаря такому обстоятельству в общем случае можно улучшить общие показатели производительчости с помощью гибридных алгоритмов.

Упражнения

7.21. Нужны ли служебные ключи, если сортировка вставками вызывается непосредственно из быстрой сортировки?

7.22. Снабдить профамму 7.1 инструментальными средствами, которые позволили бы подсчитать процент операций сравнения при разбиении файлов, размеры которых не превосходят 10, 100 и 1000 элементов, и вывести на печать значения, которые принимают это процентное отношение для случаев сортировки файлов с произвольной организацией, состоящих из N элементов для = 10, 10 *, 10 и 10

о 7.23. Реализовать рекурсивный вариант бысфой сортировки с отсечением для сортировки вставками подфайлов, размеры которых не превышают М элементов, и эмпирически определить значения М, при которых программа достигает максимального быстродействия в вашей вычислительной среде при сортировке файлов с произвольной организацией, состоящих из /V элементов для Л= 10, 10\ 10 и 10

7.24. Решить задачу, сформулированную в упражнении 7.23, воспользовавшись нерекурсивной реализацией.

7.25. Решить задачу, сформулированную в упражнении 7.23, для случая, когда сортируемые записи содержат а ключей и b указателей на другую информацию (но мы не используем сортировку по указателям).

7.26. Написать программу, которая вычерчивает гистограмму (см. профамму 3.7) для размеров подфайлов, передаваемых в сортировку вставками, при выполнении сортировки файла размером с отсечением подфайлов с размерами, не превышающими М. Выполнить эту программу для Л/ = 10, 100 и 1000 и = 10, 10 *, 10 и 10

1Ш1111111И11ШШ1ШШ1 г

РИСУНОК 7.9. СРАВНЕНИЯ В БЫСТРОЙ СОРТИРОВКЕ

Подфайлы в условиях быстрой сортировки обрабатываются независимо друг от друга. На этой диаграмме показан результат разбиения каждого подфайла в процессе сортировки 200 элементов с отсечением файлов размером 15 и меньше. Получить приближенное представление об общем числе сравнений можно, сосчитав количество отмеченных элементов в вертикальных столбцах. В рассматриваемом случае каждая позиция массива во время сортировки вовлекается только в шесть или семь подфайлов.