Программа 7.3 представляет собой нерекурсивную реализацию, которая решает данную проблему путем проверки размеров обоих подфайлов и размещения большего из них в стек первым. Рисунок 7.6 служит иллюстрацией такой стратегии. Сравнивая этот пример с приведенным на рис. 7.1, мы видим, что при такой стратегии подфайлы не меняются, меняется только порядок их обработки. Таким образом, мы сокращаем расход памяти без увеличения расхода времени.

Стратегия, которая заключается в том, что в стек помещается больший их двух подфайлов, приводит к тому, что каждая запись в стеке составляет не более чем половину записи, предшествующей ей в стеке, поэтому под стек отводится пространство памяти, достаточное для размещения примерно IgiV записей. Использование стека по максимуму имеет место, когда точка разделения приходится на середину файла. Что касается файлов с произвольной организацией, то фактический максимальный размер стека намного меньше; для вырожденных файлов его размер, по-видимому, также будет небольшим.

Программа 7.3. Нерекурсивная программная реализация быарой сортировки.

Представленная ниже нерекурсивная реализация {см. главу 5) использует явно определенный стек магазинного типа, заменяя рекурсивные вызовы помещением в стек параметров, а вызовы процедур и выходы из них - циклом, который осуществляет выборку параметров из стека и их обработку, пока стек не пуст. Мы помещаем больший из двух подфайлов в стек первым с тем, чтобы максимальная глубина стека при сортировке N элементов не превосходила величины 1дЛ/.

#include STACK.cxx

inline void push2(STACK<int> { s.push(B); s.push(A); tenlate <class Item> void quicksort(Item a[], int { STACK<int> s(50)); push2(s, 1, r); while (!s.enpty())

&s, }

1, int r)

r = s.popO ; continue;

1, r)

1 = S.popO if (r <= 1) int i = partition(a, int (i-1 > r-i)

{ push2(s, 1, i-1)

else

{ push2(9, i+1, r)

A s о R t A A E(Dt A A© A®

g E g о

A M P L S M P L

®

l i n g о p

M(g)X T S ©T X T®

g(m)o P

® P

®

@p ©

®

AAEEGILMNOPRSTX

РИСУНОК 7.6. ПРИМЕР БЫСТРОЙ СОРТИРОВКИ (ПЕРВЫМ СОРТИРУЕТСЯ МЕНЬШИЙ ПОДФАЙЛ)

Очередность, в которой производится обработка подфайлов, не препятствует корректному выполнению алгоритма быстрой сортировки и не приводит к увеличению времени выполнения сортировки, однако может повлиять на размеры стека магазинного типа, положенного в основу рекурсивной структуры. В рассматриваемом случае первым обработке подвергается меньший из подфайлов, образованных в результате каждого разделения.

int А, int В)

push2(s, i+1, г); } push2(s, 1, i-1); }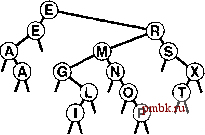

Лемма 7.3. Если меньший из двух подфайлов сортируется первым, то стек никогда не содержит более \gN вхождений в случаях, когда для сортировки N файлов применяется быстрая сортировка.

В наихудшем случае размер стека не должен превышать 7>, где 7V удовлетворяет рекуррентному соотношению 7> = Т[лу2] + 1 при Т\ = Tq = 0. Это рекуррентное соотношение является стандартным и принадлежит к типу, рассмотренному в главе 5 (см. упражнение 7.13).

Этот метод не обязательно будет работать в по-настоящему рекурсивной реализации, поскольку он зависит от очистки стека по окончании рекурсивной процедуры {end- либо tail-recursion removal). Когда последним действием какой-либо процедуры является вызов другой процедуры, то в некоторых системах программирования действует следующее соглашение: локальные переменные удаляются из стека раньше, чем произойдет такой вызов, но отнюдь не после этого. Без такой очистки нельзя быть уверенным, что размер стека, используемого быстрой сортировкой, будет небольшим. Например, вызов быстрой сортировки с целью упорядочения уже отсортированного файла размером приводит к рекурсивному вызову для упорядочения такого же файла, но размером N- \, что, в свою очередь, приводит к рекурсивному вызову для файла размером TV - 2 и так далее, для чего в конечном итоге потребуется стек с глубиной, пропорциональной N. С учетом подобного обстоятельства сам собою напрашивается вывод о необходимости использования нерекурсивной реализации, что гарантировало бы от чрезмерного разбухания стека. С другой стороны, некоторые компиляторы С++ автоматически исключают завершающую очистку стека, и многие машины обеспечивают прямую аппаратную поддержку вызовов функций - поэтому нерекурсивная реализация, представленная программой 7.3, может на самом деле в такой среде оказаться медленнее рекурсивной реализации, представленной в программе 7.1.

Рисунок 7.7 служит иллюстрацией того, как нерекурсивный метод производит обработку тех же подфайлов (но в другом порядке), что и рекурсивный метод, применительно к любому файлу. На нем показана древовидная структура, в ко-

РИСУНОК 7.7. РАЗДЕЛЯЮЩЕЕ ДЕРЕВО БЫСТРОЙ СОРТИРОВКИ

Если мы сожмем диаграммы разделения, представленные на рис. 7.6 и 7.1, соединив каждый разделяющий элемент с разделяющими элементами, использованными в двух его подфайлах, то получим показанное на данной диаграмме статическое представление процесса разделения (для обоих случаев). В этом бинарном дереве каждый подфайл представлен своим разделяющим элементом (или самим собой, если он имеет размер 1), и поддеревья каждого узла суть деревья, представляющие подфайлы после разделения. Дабы не загромождать рисунок, нулевые подфайлы на нем не показаны, хотя наши рекурсивные версии алгоритма выполняют рекурсивные вызовы при выполнении условия г<1, когда разделяющим элементом становится наименьший или наибольший элемент файла. Само по себе дерево не зависит от очередности, в которой подфайлы подвергаются разделению. Наша рекурсивная реализация сортировки соответствует посещению узлов при их обходе в прямом порядке, а нерекурсивная реализация соответствует правилу посещения сначала наименьшего дерева.

тором корневым элементом служит разделяющий элемент, а также порожденные при этом левое и правое поддеревья, соответствующие левому и правому подфайлам и являющиеся, соответственно, левым и правым потомками. Использование рекурсивной реализации, представленной программой 7.3, соответствует просмотру этих узлов в прямом порядке; нерекурсивная реализация соответствует правилу просмотра сначала наименьшего дерева.

Когда используется явно заданный стек, что, собственно говоря, и делалось в программе 7.3, удаётся избегать некоторых непроизводительных затрат, характерных для рекурсивных реализаций, хотя современные системы программирования не привносят больших непроизводительных затрат в столь простые программы. Программу 7.3 можно улучшать и дальше. Например, она помещает в стек оба подфайла, но только подфайл, хранящийся в вершине стека, доступен в любой момент; такое положение дел можно изменить, явно объявив специальные переменные г и 1. Итак, производится проверка условия г < 1 по мере того, как подфайлы выбираются из стека, в то время как намного эффективнее вообще не сохранять в стеке файлы, удовлетворяющие упомянутому условию (упражнение 4.14). Эта мера, на первый взгляд, может показаться несущественной, однако рекурсивный характер быстрой сортировки фактически приводит к тому, что значительная часть подфайлов в процессе быстрой сортировки имеет размеры 1 или 0. Далее рассматривается важное усовершенствование быстрой сортировки, которое обеспечивает повышение ее эффективности за счет распространения этой идеи на все файлы небольших размеров.

Упражнения

> 7.11. В стиле рис. 7.11 представить содержимое стека после каждой пары операций помещения {push) в стек и выталкивания {pop) из стека, когда программа 7.3 используется для сортировки файла, содержащего ключи EASYQUESTION.

[> 7.12. Выполнить задание, сформулированное в упражнении 7.11, для случая, когда в стек сначала помещается правый подфайл, а затем левый подфайл (как это принято в рекурсивной реализации).

7.13. Завершить доказательство леммы 7.3, воспользовавшись для этой цели методом индукции.

7.14. Внесите в программу 7.3 такие изменения, чтобы она не помещала в стек подфайлы, удовлетворяющие условию г <= 1.

[> 7.15. Вычислить максимальный размер стека, затребованного программой 7.3, когда N = 2 .

7.16. Вычислить максимальные размеры стека, затребованного программой 7.3, когда Л= 2 - 1 и N=2 + \.

о 1Л1. Имеет ли смысл использовать для нерекурсивной реализации быстрой сортировки вместо стека очередь? Предъявите аргументы для обоснования своих ответов.

7.18. Выясните и сообщите, практикует ли ваша система программирования очистку стека по завершении рекурсивной процедуры.