О После вызова интервал перестает быть ьсучей.

О Перед вызовом необходимо проследить за тем, чтобы элементы в интервале [beg,end-l) формировали кучу (с общим критерием сортировки).

О Сложность логарифмическая (не более number ОfElementsyXognumberOf-Elements) сравнений).

Пример использования алгоритмов для работы с кучей

Следующая программа демонстрирует использование различных алгоритмов работы с кучей:

algo/heapl.cpp #include algostuff.hpp using namespace std;

int mainO {

vector<int> coll:

INSERTJLEMENTSCcoll .3.7) IN5ERTJLEMENTS(coll .5.9) lNSERT ELEMENTS(coll.l.4)

PRINT ELEMENTS (coll. on entry: );

Преобразование коллекции в кучу make heap (coll.beginO. coll.endO);

PRINTJLEMENTS (coll. after make heap(); );

Извпечение следующего элемента из кучи popjeap (coll .beginO, coll.endO); coll. pop Jack О:

PRINTJLEMENTS (coll. after popJeapO; );

Занесение нового элемента в кучу coll.push back (17): pushjeap (coll .beginO . coll.endO);

PRINTJLEMENTS (coll, after push heap(): );

/* Преобразование кучи в упорядоченную коллекцию * - ВНИМАНИЕ; после вызова интервал перестает быть кучей */

sortjeap (coll .beginO. coll.endO); PRINTJLEMENTS (coll. after sortJeapO; );

Результат выполнения программы выглядит так:

СП entry: 34567567891234

after make heap(): 98677553641234

after pop heap(): 8767455364123

after push heap(): 17 7874563641235

after sort heap(): 1233445566778 17

После вызова make heap() элементы сортируются в виде кучи:

98677553641234

Если преобразовать эту последовательность в бинарное дерево, вы увидите, что значение каждого узла меньше либо равно значению его родительского узла (рис. 9.1). Алгоритмы push heap() и pop heap() изменяют элементы так, что инвариант структуры бинарного дерева (любой узел не больше своего родительского узла) остается неизменным.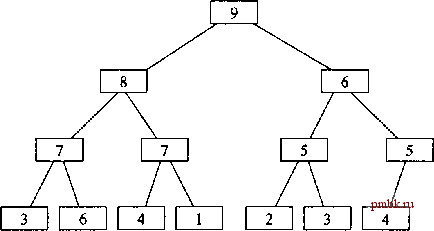

Рис. 9.1. Элементы кучи в виде бинарного дерева

Алгоритмы упорядоченных интервалов

Алгоритмы упорядоченных интервалов требуют, чтобы элементы исходных интервалов были упорядочены по своим критериям сортировки. Обычно эти алгоритмы работают гораздо эффективнее своих аналогов для неупорядоченных интервалов (как правило, они обладают логарифмической, а не линейной слож-гюстью). Алгоритмы упорядоченных интервалов могут использоваться с итераторами, которые не являются итераторами произвольного доступа, но в этом случае сложность оказывается линейной, поскольку им приходится последовательно перебирать элемент за элементом. Впрочем, количество сравнений все равно может остаться логарифмическим.

Согласно стандарту, вызов этих алгоритмов для незшорядоченных интервалов приводит к непредсказуемым последствиям. Хотя в большинстве реализаций алгоритмы успешно работают с неупорядоченными последовательностями, использовать их в программе нельзя - это нарушит ее переносимость.

В ассоциативных контейнерах определены специальные функции, аналогичные по назначению представленным далее алгоритмам. При поиске по заданному значению или ключу следует использовать эти функции вместо алгоритмов.

Поиск элементов

Следующие алгоритмы предназначены для поиска значений в упорядоченных интервалах.

Проверка npMqfrcTBMfl элемента

bool

binary search (Forwardlterator beg. Forwardlterator end. const T& value) bool

binary search (Forwardlterator beg. Forwardlterator end. const T& value. BinaryPredicate op)

О Обе формы проверяют, содержит ли упорядоченный интервал [beg,end) элемент со значением value.

О В необязательном параметре ор передается бинарный предикат, определяющий критерий сортировки: op(elem1,elem2).

О Чтобы определить позицию искомого элемента, воспользуйтесь функциями lower bound(), upper bound() и equal range() (см. с. 402).

О Перед вызовом интервал должен быть упорядочен по соответствующему критерию сортировки.

О Сложность логарифмическая для итераторов произвольного доступа, линейная в остальных случаях (не более \og(numberOfElements)+2 сравнений, но для итераторов, не являющихся итераторами произвольного доступа, выполняется линейное количество операций перебора, вследствие чего сложность оказывается линейной).

Пример использования алгоритма blnarv search():

algo/bsearchl.cpp #1nclude algostuff-hpp using namespace std:

int mainO

list<1nt> coll:

INSERT ELEMENTS(coll,1,9): PRiNTJLEMENTSCcoll):

Проверка существования элемента со значением 5 if Cbinary searchCcon,beginO. coll.endC). 5)) ( cout 5 is present endl: