Козьма Прутков настойчиво напоминает: нельзя объять необъятное! Почти каждая задача из этой книги иллюстрирует какой-либо принцип, достойный отдельной главы. Однако объём книги не беспределен, да и кругозор автора тоже. Поэтому неудивительно, что некоторые вполне самостоятельные темы оказываются представленными всего лишь двумя-тремя задачами. Таким темам и посвящена эта глава.

Описываемые задачи объединены в четыре группы: стратегии для игр , анализ и обработка изображений , стеганография и специализированные алгоритмы .

В разделе стратегии для игр Мы изучим устройство оптимальных алгоритмов компьютерного игрока в различных известных играх, таких как Мастермайнд, шахматы (разыгрывание простого эндшпиля) и Minesweeper.

Часть, озаглавленная анализ и обработка изображений посвящена некоторым специальным алгоритмам, работающим с чёрно-белыми изображениями. Речь пойдёт, в частности, о преобразовании изображений (обрезка и поворот), их анализе (см. п. 9.2.3 Жесты мыши ) и сжатии.

Под заголовком стеганография объединены задачи, посвященные интересному методу сокрытия секретной информации - стеганографии. Думаю, многие читатели услышат о нём впервые.

В секции специализированные алгоритмы обсуждаются методы специального вида, предназначенные для решения нестандартных задач. Иногда они базируются на весьма общих принципах, широко используемых на практике (например, в п. 9.4.1 Оптимальное вычисление применяется принцип динамического программирования).

9.1. СТРАТЕГИИ ДЛЯ ИГР

9.1.1. Мастермайнд

Разработка стратегии для классической игры

Написать программу, способную играть в классическ)ш логическую игру Мастермайнд на стороне любого из противников.

Загадывающий игрок набирает ряд из четырёх цветных фишек (цвета в ряду могут повторяться сколько угодно раз; всего доступно шесть различных цветов). Отгадывающему игроку предоставляется десять попыток, чтобы определить набранный соперником ряд. Во время очередного хода отгадывающий выставляет на доске свою версию ряда, а загадывающий с помощью чёрных и белых отметок указывает, насколько отгадывающий приблизился к правильному ответу.

Белая отметка указывает, что в текущем ряду отгадываюгцего есть фишка требуемого цвета, но она находится на неверной позиции (рис. 9.1).

подсказки ряд отгадывающего

ПоПо]

ряд загадывающего Рис. 9.1. Мастермайнд: белая отметка

В ряду загадывающего есть белая фишка (это правильно), есть и чёрная (тоже правильно), но находятся они на неверных позициях. Заметьте, что расположение чёрно-белых отметок - произвольное, оно не объясняет, какие именно фишки найдены в загаданном ряду.

Чёрная отметка указывает, что в текущем ряду отгадывающего есть фишка требуемого цвета, и она находится на корректной позиции (чёрная, рис. 9.2).

Пожалуй, единственный неоднозначный момент в расстановке подсказок связан с повторяющимися цветами в ряду отгадывающего. Предположим,

подсказки

ряд отгадывающего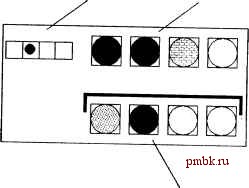

ряд загадывающего Рис. 9.2. Мастермайнд: черная отметка

загадан ряд из трёх белых фишек и одной чёрной. Отгадывающий ставит три чёрные фишки на неверных местах и одну серую. Сколько белых подсказок должно быть установлено? Здесь действует такая логика: поскольку в решении нужна всего одна чёрная фишка, мы считаем, что соперник угадал её существование, но не угадал позицию (то, что он не угадал три раза, сути дела не меняет). Таким образом, будет установлена всего одна белая подсказка.

Конечно, Мастермайнд - игра хорошо изученная. Для отгадываюп1его игрока существуют хорошие стратегии. Однако я не буду лишать вас удовольствия поразмыслить над ними самостоятельно.

Подсказка

Хотя ещё в семидесятых годах Дональд Кнут предложил стратегию, гарантировано разгадывающую любую комбинацию фишек за пять ходов, альтернативные решения предлагаются по сей день. Дело в том, что некоторые алгоритмы могут давать лучшие результаты в среднем, допуская при этом редкие осечки . Так, К. Коуаша и Т. W. Lai разработали алгоритм, требующий в среднем 4.340 хода, но на некоторые комбинации затрачивающий целых шесть ходов.

Здесь я опишу на псевдокоде решение, приведённое в ВикипедииЧ По-видимому, алгоритм наподобие этого и был предложен Кнутом, но точной информации на этот счёт у меня нет.

Первым делом следует представить в виде множества S набор всех допустимых секретных комбинаций цветных фишек. Поскольку фишек всего че-

1296, что для

На данный момент этот алгоритм удалён из статьи об игре в Мастермайнд.

тыре, а разных цветов шесть, число комбинаций равно 6 современных компьютеров совсем немного. Предположим теперь, что отгадывающий (то есть компьютер) уже сделал ряд попыток, и мы располагаем их результатами (конфигурациями белых и чёрных отметок). В начале игры число сделанных ходов, конечно, равно нулю.

На первом шаге алгоритма требуется определить все комбинации, противоречащие полученным ранее подсказкам, и удалить их из множества S. На втором шаге печатается ответ, если множество S содержит единственный элемент. Если множество S пусто, это значит, что в процессе игры загадывающий допустил какую-либо ошибку при установке подсказок, и задача более не имеет решений.

На третьем шаге (до которого алгоритм дойдёт, только если множество S содержит более одного элемента) некоторым образом выбирается следующий ход отгадывающего из множества S, а управление переходит к первому шагу.

Если первый и второй шаги более-менее реализуемы, третий скрывает в себе всю суть алгоритма игры. Как уже упоминалось выше, существуют различные схемы выбора наилучшего хода. Разумно выбрать комбинацию, приводящую к максимальному уменьшению множества S. Для этого придётся просмотреть все не противоречащие текущей ситуации попытки в поиске наилучшей кандидатуры. Впрочем, как показывают опыты, даже простейший случайный выбор способен разгадать комбинацию в среднем за 4.6 хода, что мне представляется вполне удовлетворительным решени-ем. Автор этого подхода, впрочем, указывает, что случайный выбор может привести к партии длиной даже в 8 ходов (по его оценке вероятность такого исхода не превышает 0.05%).

9.1.2. Эндшпиль

Формализация алгоритма матования

Требуется написать программу, способную заматовать одинокого короля, управляемого человеком, с помощью ладьи и короля. Первый ход предоставляется чёрным. Начальная расстановка фигур фиксирована: чёрный король на Е5, белый король на D1, белая ладья на Н2. Дополнительное задание: решить задачу для произвольной расстановки фигур, вводимой с клавиатуры.

С++ MacYep-класс. 85 нетривиальных проектов, решений и задач Решение

Здесь я приведу решение лишь для жёстко заданной начальной расстановки фигур, указанной в условии: белый король на D1, белая ладья на Н21, чёрный король на Е5.

Общей процедурой рситения шахматных энд1ппилей является так называемый ретроградный анализ - просмотр позиций н обратном порядке (от матовых к позициям мат в один ход и так далее до того, пока пе встретится текущее расположение). Однако эндшпиль к()роль-ла;1ья-король очень прост, и стрельба из пупгки но воробьям здесь вряд ли оправдана.

К счастью, существует совершенно чёткий алгоритм, приводящий к победе белых. На неформальном уровне он выглядит так.

Для начала следует выбрать любой из краёв доски, к которому будет оттесняться чёрный король. В моём решении используется верхний край, то есть восьмая горизонталь.

Теперь ладья должна перекрыть чёрному королю дорогу к противоположному краю доски, переместившись на горизонталь, предшествующую горизонтали короля (чёрные: Кр f5, белые: Л h4; рис. 9.3).

Рис. 9.3. Оттеснение черного короля

Следующий шаг - продвижение белого короля на третью горизонталь (предшествующую горизонтали ладьи). Разумеется, в случае возникновении угрозы ладье со стороны чёрного короля ладью необходимо переместить в безопасную клетку на той же горизонтали.

Далее, действуя совместно, белые должны добиться возникающей после хода чёрных ситуации оппозиции, то есть расположения разделённых одной свободной клеткой королей на одной вертикали (рис. 9.4).

Рис 9.4. Оппозиция королей

Очередным ходом (Л h5) белые вынуждают чёрного короля сдвинуться ближе к краю доски. Если король уже находится на восьмой горизонтали, игра заканчивается победой белых.

Осталось запрограммировать этот алгоритм, содержащий некоторое количество подводных камней.

Начнём с описания начального расположения фигур на поле:

pair<char, int>BK(e, 5), WK(d, 1), WR(h, 2);

чёрный король белый король белая ладья

Для удобства работы с программой нам потребуется функция, выводящая на экран текущую ситуацию на доске:

void PrintBoardO {

белую клетку изображает пробел, черную - символ OxDB -

закрашенный прямоугольник

char S[] = { char(OxDB), , char(OxDB) );

цикл no горизонталям for(int i = 8; i >= 1; i-) {

cout i; цикл no вертикалям for(char j = a; j <= h; j++) {

pair<char, int> c(j, i); текущая позиция

if(WK == c) cout -WK ; если там белый король else if(BK == с) cout ВК ; чёрный король else if(WR == с) cout WR ; белая ладья

номер горизонтали