cqueue.Update(); Draw();

Очень интересную картину можно наблюдать при следующих начальных данных:

допустимая скорость = 80 (км/ч) частота генератора автомобилей = 5 (сек) допустимая дистанция = 40 (м) частота генератора помех = 15 (сек)

Если у какой-либо машины случается поломка, то ещё в течение нескольких итераций в этом месте можно наблюдать сгущение машин (собственно, пробку), которое с течением времени рассасывается (рис. 7.6).

Автостраяа. атоблн. айв а

=> о о о о о о* оооооооосоооооо о о* о о о* о о о о о осо* оо о*

Длмнапатм[км) \\ Дйпасгшиаяскоростьаатомойияейкм/ч Машжн<(тра(хв-,4Б -

[во Прошло машин: 2

Частота генератора адгомо<нл й [cenj Допастнмая диааниия (м) Скорость мсмели Пропужная способность:

5 Р5--f\d 2 .1вминвr!j

Часгготапицлио помех (сек) ч,-,-

Рис. 7.6. Возникновение пробки на дороге

7.2.6. Змейки-лесенки: экспериментальный анализ игры

Эта игра (рис. 7.7) в том или ином виде существует уже не первую сотню лет. Уверен, многие из вас немало времени потратили на что-либо подобное в детстве.

В игре участвует сколько угодно человек. Изначально фишки игроков ставятся на клетку с номером 1. Затем участники по очереди бросают кубик и передвигают свои фишки на выпавшее на кубике количество клеток вперёд. Если фишка остановилась на клетке, с которой начинается *лесенка (например, 2, 4, 10; конечные клетки *лесенок вроде 22 или 37 к таковым не относятся), она автоматически переносится на клетку, в которую лесенка ведёт. Змейка , наоборот, переносит игрока назад (от головы к хвосту). Игра заканчивается, как только один из игроков достиг финишной клетки (даже если на кубике выпало больше очков, чем требуется). Он и объявляется победителем.

Теперь нам предстоит провести компьютерный анализ игры. Задача достаточно проста. Требуется сыграть достаточное количество партий (несколько сотен), в которых участвует лишь один человек. Затем следует вывести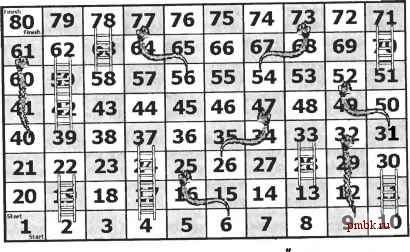

Рис. 7.7. Игра Змейки-лесенки

гистограмму, иллюстрирующую распределение количества ходов, необходимых для завершения игры. Так, высота столбца с номером к показывает, сколько партий закончилось на к-м ходу.

7.3. БИОЛОГИЧЕСКИЕ МОДЕЛИ

7.3.1. Волчий остров. Классическая биологическая моДель

Эта и следующая задачи описаны у Д. Ван Тассела . Где-то в океане находится Волчий остров, имеющий форму квадрата, разделенного на 20x20 = 400 клеток. Население острова составляют кролики, волки и волчицы. Изначально остров случайным образом заселяется представителями каждого вида (по нескольку особей). Обратите внимание, что в любом квадрате может одновременно находиться несколько животных.

На каждом шаге моделирования производятся следующие действия:

Каждый кролик случайным образом перемещается в одну из восьми соседних клеток (выход за пределы острова, естественно, невозможен) или остаётся на месте. Вероятность любого исхода одинакова.

С вероятностью 0.2 каждый кролик размножается (видимо, делением), превращаясь в двух кроликов.

6 Dennie Van Tassel. Program style, design, efficiency, debugging, агк1 testing. 2nd ed. Prentice-Hall,

NJ. 1978 (русский перевод: Д. Ван Тассел. Стиль, разработка, эффективность, отладка и испытание программ, 2-е изд. Москва. Мир. 1985).

Каждая волчица передвигается слзгчайным образом, если в ближайших клетках нет кроликов. Если же в одной из восьми соседних клеток обнаруживается кролик, волчица начинает на него охоту , то есть целенаправленно перемещается в клетку, содержащую кролика. Если волчица оказывается в одной клетке с кроликом, она его съедает и получает одну единицу энергии. Любой холостой ход без поедания добычи отнимает у волчицы 0.1 единиц энергии.

Волк ведёт себя аналогично волчице. Если ни в одной из соседних клеток нет кроликов, но есть волчица, волк направляется за ней. Если волк и волчица оказываются в одной клетке, не содержащей кролика, они производят потомка случайного пола (характерно, что еда имеет приоритет перед продолжением рода).

Изначально каждый волк и каждая волчица имеют по одной единице энергии. Животные, растерявшие всю свою энергию, погибают (исчезают с острова).

Задание заключается в моделировании жизни на Волчьем острове в течение некоторого промежутка времени.

Автор модели заметил, что обычно волки и волчицы довольно быстро истребляют всю популяцию кроликов, после чего погибают от голода (вот к чему приводит жадность). Модель можно сделать более сбалансированной, если пометить небольшой квадрат внутри острова как кроличью ферму , куда ход волкам запрещён.

7.3.2. Инфекция стригущего лишая Ещё одна модель из биологии

Несмотря на зловещее и, быть может, даже отпугивающее название, с точки зрения исследования эта модель очень интересна.

Задача заключается в моделировании процесса распространения инфекции стригущего лишая по участку кожи размером NN клеток (N - нечётное число).

Инфекция начинается с центральной клетки участка. В каждый момент времени поражённая инфекцией клетка с вероятностью 1/2 заражает любую из восьми соседних здоровых клеток. Через шесть итераций моделирования заражённая клетка становится невосприимчивой к инфекции, а ещё через четыре итерации - здоровой.

В процессе моделирования требуется выводить на экран схему участка кожи, отмечая разными цветами заражённые, здоровые и невосприимчивые к инфекции клетки.

Решение

Начнём с описания участка кожи размером NxN клеток:

enum STATE { HEALTHY, INFECTED, IMMUNE }; состояние клетки

клетка

struct Cell {

STATE State; int Count;

её состояние

и счётчик итераций

Cell(STATE state = HEALTHY, int count = 0)

: State( state), Count( count) {}

int N;

vector<vector<Cell> > Skin; участок кожи

Счётчик итераций помогает отследить момент времени, когда клетка становится невосприимчивой к инфекции или здоровой.

Поскольку задача связана с выводом графики, я предполагаю, что из приложения доступна главная форма (MainForm), на которой находится элемент DrawingArea типа TImage, две кнопки btnReset и btnStep, а также поле ввода edSize.

Кнопка btnReset инициализирует участок кожи NxN с инфицированной центральной клеткой:

void fastcall TMainForm::btnResetClick(TObject *Sender)

размер участка кожи

N = atoi(edSi2e->Text.c str());

Skin.resize(N +2);

for(int i = 0; i <= N + 1; i++)

Skin[i].resize(N +2);

все клетки здоровы

for(int j = 1; j <= N; j++)

Skin[i][j].State = HEALTHY;

центральная клетка заражена

Skin[N / 2 + 1][N / 2 + 1] = Cell(INFECTED. 6); обновить содержимое экрана UpdateScreen(); randomize();

Чтобы не возникало проблем с выходом за границы массива при обработке близких к краям клеток, я искусственно расширил размеры с NxN

до (N + 2) X (N + 2) (при этом реально будут использоваться координаты [1...N, 1...N]).

Функция обновления экрана UpdateScreen () перерисовывает текущее состояние участка кожи, закрашивая клетки цветами: здоровая - белый, инфицировавшая - красный, невосприимчивая - зелёный.

void UpdateScreen() {

размеры клетки в пикселях

double Сх = MainFonn->DrawingArea->Width / (double)N, Су = MainForin->DrawingArea->Height / (double)N;

for(int i = 1; i <= N; i++)

for(int j = 1; j <= N; j++) {

TColor с = Skin[i][j].State == HEALTHY ? clWhite :

(Skin[i][j].State == INFECTED ? clRed : clGreen); нарисовать закрашенный прямоугольник MainForm->DrawingArea->Canvas->Brush->Color = с; MainFonn->DrawingArea-OfCanvas->FillRect(Reet((il)*Cx. (jl)*Cy,

i*Cx, j*Cy));

и чёрную кайму вокруг

MainFonn->DrawingArea->Canvas->Brush->Color = clBlack; MainForm >DrawingArea >Canvas->FraineRect(Rect((i 1)*Cx, (j 1)*Cy,

i*Cx, j*Cy));

Нажатие кнопки btnStep запускает процедуру шага моделирования:

void fastcall TMainForm::btnStepClick(TObject *Sender)

цикл no всем клеткам for(int i = 1; i <= N; i++)

for(int j = 1; j <= N; j++)

если клетка невосприимчива и ей пора выздороветь, делаем клетку здоровой if(Skinii][j].State == IMMUNE) if(--Skin[i][j].Count == 0)

Skin[i][j].State = HEALTHY;

если клетка заражена и должна стать невосприимчивой, делаем клетку невосприимчивой на четыре итерации if(Skin[i][j].State == INFECTED) if(--Skin[i][j].Count == 0)

Skin[i][j] = Cell(IMMUNE, 4);

список клеток, подлежащих заражению list<pair<int, int> > Tolnfect;

циклено всем клеткам for(int i = 1; i <= N; i++) for(int j = 1; j <= N; j++)

if(Skin[i][j].State == INFECTED) {

если клетка заражена, рассматриваем соседние: с вероятностью 1/2 каждая соседняя здоровая клетка попадает в список Tolnfect for(int X - i - 1; X <= i + 1; x++) for(int у = j - 1; у <= j + 1; У++)

if (Skin[x] [y]-State == HEALTHY && randoin(2) ==

Tolnfect.push back(pair<int, int>(x, y));

делаем каждую клетку из списка Tolnfect зараженной на б итераций

for(list<pair<int, int> >::iterator p = Tolnfect.begin();

p != ToInfect.endO; p++) Skin[p->first][p->second] = Cell(INFECTED, 6);

UpdateScreen0;

Результат работы программы после пятнадцати итераций моделирования показан на рис. 7.8. ШШШШШШШШШЩШШШШШШШЛЛ

step

Рис. 7.8. Модель инфекции стригущего лишая