return words[random(words.size О ) ] ;

Здесь используется уже знакомая вам идея из решения п. 6.2.1 ( Самообучающиеся крестики-нолики ): в массив words записывается несколько копий каждого слова таблицы в пропорциях, соответствующих отношениям вероятностей, а затем из массива выбирается случайный элемент.

Генерацией текста занимается функция main ():

int mkin(int argc, char* argv[]) {

string filename; randomize();

считать входные параметры

cin К;

cin N;

cin filename;

создать таблицу вероятностей

Analyze(filename);

выбрать случайный элемент таблицы (список из К слов) map<list<string>, map<scring, double> >::iterator start = Prob.begin{); advance(start, random(Prob.size()));

сделать его стартовым list<string> CurKey = start->first;

copy(CurKey.begin 0, CurKey.end(), ostream iteratcr<string>(cout. * -));

сгенерировать и вывести на экран оставшиеся N - К слов

for(unsigned i = 0; i < N - К; i++)

string temp = GetRandomWord(Prob[CurKey]); CurKey.push back(temp); CurKey.pop front(); cout temp ;

return 0;

В качестве примера приведу фрагмент текста, сгенерированного программой на основе книги Так говорил Заратустра Фридриха Ницше (К = 2):

До сих пор, что человеку нужно его самое злое так ничтожно! Ах, его самое злое для его несовершенного Творца, - таким стоял мир на моей горе Елеонской; в освещенном солнцем уголку моей горы Елеонской пою и смеюсь я над моей суровою гостьей и благодарен ей еще за то, что каждый вносит в него, даже внутренняя скотина. Поэтому отговариваю я многих от одиночества.

7.2. КОМПЬЮТЕРНЫЕ ЭКСПЕРИМЕНТЫ

7.2.1. Экспериментальное определение числа п. Использование метода Монте-Карло

Значение числа к с некоторой степенью точности можно определить с помощью эксперимента. Возьмём квадрат со стороной 2г и впишем в него круг. Теперь нанесём на чертёж большое количество точек в случайных местах квадрата. При достаточно большом их количестве отношение общего числа точек (N) к числу точек, попавших внутрь круга (N), будет примерно равно отцошению площадей квадрата и круга:

* S /S

о квадрата круга

Поскольку Sp = (2тУ, а S = тп-, значение л можно получить по формуле:

п 4

Задача заключается в экспериментальном определении числа л этим способом.

Подобная имитация случайных процессов называется методом Монте-Карло и широко применяется при решении самых разных задач в физике, экономике и в других науках.

7.2.2. Доска Гальтона. Моделирование распределения Гаусса

Случайные величины, с которыми приходится иметь дело при анализе задач, подчиняются разным законам распределения. Бросая кубик, мы ожидаем, что каждое из шести указанных на гранях чисел выпадает с одной и той же вероятностью. Брюсая два кубика одновременно, разумно ожидать, что сумма выпавших чисел будет чаще равна трём и реже - двум (потому что в первом случае годятся варианты 1-2 и 2-1, а во втором - лишь 1-1). Для демонстрации очень часто возникающего на практике нормального (га-уссовского) распределения (рис. 7.1) случайных величин можно использовать доску Гальтона.

С++ мастер-класс

вероятность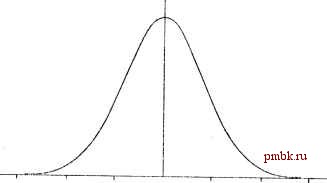

случайная величина

Рис. 7.1. Нормальное распределение случайной величины

Это устройство представляет собой гладкую поверхность (доску), на которой расположено несколько рядов клинышков. Первый ряд состоит лишь из одного клинышка, второй из двух, третий из трёх и так далее (рис. 7.2).

Хотя здесь изображена доска из четырёх рядов, вообще говоря, их количество ограничивается лишь трудолюбием автора. Наша промышленность, кстати, выпускает такие доски для нужд учебных заведений (стоимость одной доски составляет более 44 ООО (!) рублей).

Доска размещается вертикально. Сверху опускается круглая фишка или монетка. С вероятностью 50% она падает налево или направо, после чего попадает на один из клинышков второго ряда. Процесс продолжается, пока фишка не достигнет одного из желобков, расположенных на нижнем краю доски (если доска состоит из N рядов, в итоге фишка может закончить падение в одном из N+1 положений).

□ О Q О G

J U

Рис. 7.2. Доска Гальтона

ISaJaUausj.

Глава 7. Моделирование вероятностных процессов

При достаточно большом количестве экспериментов распределение фишек в желобках будет в той или иной степени соответствовать нормальному распределению.

Подозреваю, что далеко не все имеют желание покупать и устанавливать у себя в кабинете такую штуковину. Поэтому предлагается смоделировать доску Гальтона на компьютере.

Пользователь вводит с клавиатуры количество рядов доски и число проводимых испытаний. Компьютер выполняет моделирование (желательно вывести апимировшпгую схему), а затем выводит гистограмму, иллюстрирующую распределение фишек в желобках на краю доски.

7,2.3. Автобусная остановка

Экспериментальная проверка гипотезы

Представьте себе картину: холодный ноябрьский вечер, вы стоите на автобусной остановке, переминаясь с ноги на ногу, и мечтаете поскорее попасть домой, где вас уже ждёт горячий чай с конфетами или, быть может, что-1шбудь покрепче. Наконец вы замечаете автобус, но, как назло, едет он в противоположную сторону.

Вероятно, люди, профессионально разбирающиеся в психологии, скажут, что мы склонны обращать внимание на происшествия неприятные, в то время как мелкие удачи проходят незамеченными. Таким образом, всевозможные законы бутерброда порождены скорее нашим воображением, чем истинным положением вещей.

-Тем не менее, в случае с автобусной остановкой закон бутерброда действительно работает, если сделать несколько нехитрых предположений.

Итак, предположим, что единственный автобус курсирует между пунктами А и В с постоянной скоростью. Достигнув конечного пункта, автобус разворачивается и едет по той же самой дороге в обратном направлении. В случайный момент времени человек выходит на остановку, расположенную в случайной точке С маршрута автобуса.

Остановка, куда собирается ехать человек, находится в другой случайной точке маршрута - назовём её D. Утверждается, что проезжающий мимо автобус с большей вероятностью направляется в сторону, противоположную интересующей.

Эту задачу можно решить и математически, но прибережём такое решение для задачника по математике. Здесь же я предлагаю написать программу, моделирующую приведённую ситуацию. Пользователь вводит длину марш-

рута (N) в километрах, длительность дня (то есть длину промежутка времени, в течение которого пассажир может выйти на остановкуи количество экспериментов.

Скорость автобуса считается единичной (один километр в единицу времени). Компьютер печатает, сколько раз пассажиру повезло, а сколько раз - нет.

Решение

Решается эта задача довольно просто. Самое главное, что нам гютре-буется - это формула, определяющая положение автобуса на маршруте в любой данный момент времени t:

X{t) = t - int{t/2*N)*2*N

Поскольку автобус курсирует по одному и тому же маршруту длиной 2 *N, его положение в момент времени t совпадает с положением в момент времени t + 2*N (не забывайте, что автобус движется с единичной скоростью). Количество совершённых автобусом полных кругов (А - В - А) равно int (t /2*N), а соответствующее им расстояние - int (t / 2*N) *2*N. Вычитая из t эту величину, получаем текущее положение автобуса на маршруте.

Теперь обсудим, как определить, совпадает ли направление автобуса, приближающегося к остановке, с желаемым. Здесь потребуется рассмотреть два варианта в зависимости от того, куда направляется пассажир (рис.7.3).

Если человек едет в сторону пункта В (то есть С < D), то удачному положению автобуса соответствует отрезок [А, С]. Аналогично для случая С > D удачным отрезком будет [С, В].

Осталось только прямолинейно запрограммировать процедуру моделирования:

int N, DayLen, Tries;

cin N; длина маршрута

cin DayLen; длительность дня

cin Tries; количество итераций моделирования

int succ count =0; количество удачных попыток randomize();

for(int i = 0; i < Tries; i++) {

определить исходную точку int С = random(N +1);

1 Если длина дня равна DayLen, то время выхода на остановку можно выбрать как

random(UayLen).

С D В А D С

Рис. 7.3. Возможные нщправления движения пассажира

int D;

определить точку назначения while((D = random(N +1)) == С)

С != D

int t = random(DayLen); время выхода на остановку

int bus pos = t - (t / (2*N)) * 2 * N; положение автобуса

если автобус расположен удачно

if((C < D && bus pos <= С) II (С > D && bus pos >= О) succ count++;

вывод общего количества удачных и неудачных попыток, а также

их отношения друг к другу в процентах

cout succ count << / (Tries - succ count);

cout С 100*succ count/Tries % /

(100 - 100*succ count/Tries) %) ;

Пример входных и выходных данных:

50 10

5000

2160 / 2840 (43% / 57%)

7.2.4, Прокси-сервер

Использование неравномерно распределённых случайных величин

Рассмотрим вполне реалистичную ситуацию из жизни.Интернет-провай-дер покупает трафик по цене X копеек за мегабайт, а продаёт своим клиентам по цене Y копеек за мегабайт (ясное дело, Y > X). Чтобы увеличить свои доходы, провайдер решил установить у себя прокси-сервер, кэширующий запрашиваемые пользователями документы. Если кто-то попытается скачать файл, хранящийся на прокси-сервере, провайдеру уже не придётся запрашивать его из интернета: достаточно вернуть пользователю локальную копию. Провайдер ничего не заплатит за эту операцию, а с клиента возьмут по полной таксе - Y копеек за мегабайт.