в ЫВ;0;Д 4,

i : . ...1-

М:~я

вывод

к S3

о вывод

-f.........

..........i

Рис 4.13. Королевская балда (начало игры)

Игра завершается при заполнении последней клетки поля либо при возникновении ситуации, когда ни один из игроков не может сделать ход. Выигрывает тот, у кого больше очков.

Обычно в балде допускаются лишь существительные в именительном падеже, единственном числе. В программе должна быть предусмотрена функция пополнения словаря: если человек составляет слово, неизвестное компьютеру, компьютер добавляет его в свою базу данных. Для игры можно использовать простую жадную стратегию : на очередном ходе выбирается слово, даюп1ее наибольший прирост очков (даже если это грозит упущенными возможностями в будущем).

Подсказка

Очевидное решение заключается в использовании методики, описанной в задаче 4.2.1. На псевдокоде её адаптация выглядит следующим образом:

ЦИКЛ ПО всем свободным клеткам поля, смежным с какой-либо заполненной; клеткой

цикл по всем буквам русского алфавита

; построить список цепочек клеток, включающих текущую клетку выбрать из цепочек коррект-ные слова (из словаря итры) (*) л; КОНЕЦ ЦИКЛАМ

КОНЕЦ ЦИКЛА \ : ..... ,;. .. v

Числа, расположенные за пределами поля, являются подсказками; они известны заранее. Подсказки говорят, сколько наборов подряд идущих закрашенных клеток находятся на данной горизонтали/вертикали, и какова длина каждой из них. Так, слева от самой верхней горизонтали написаны числа 2 и 2. Это означает, что горизонталь содержит два набора по две закрашенные клетки в каждой.

Программа должна считывать файл с подсказками (хранящийся в любой удобной форме) и выводить пользователю решение головоломки.

Подсказка

Решение в лоб заключается в программировании простой функции перебора с возвратами (см. п. 4.2.1). По-видимому, любой разумный алгоритм так или инкче будет использовать перебор, однако оптимизировать его не так легко.

Анализу приёмов сокращения перебора в японских кроссвордах посвящена статья Ильи ПОрублёва Решения японского кроссворда , расположенная по адресу http: algolist.manual.ru/misc/ japancross.php.

4.2.3. Игра Королевская балда

Поиск наилучшего хода в игре

Итак, требуется написать программу для игры в королевскую балду . Играет человек против компьютера. Начинает компьютер. В середине поля размером 5x5 клеток пишется слово из пяти букв. Человек должен придумать новое слово, состоящее из Находящихся на поле букв и обязательно одной новой (добавляемой на поле) буквы.

На уровне интерфейса это выглядит так. Компьютер позволяет человеку поставить букву в любую свободную клетку, затем человек указывает (например, последовательно прощёлкивая мышью клетки), каким именно образом новое слово следует читать. Слова могут образовываться из букв, расположенных последовательно в любом направлении от клетки к клетке вверх, вниз, влево или вправо, но не по диагонали и без самопересечений.

Чем длиннее новое слово, тем больше очков за него даётся (по очку за букву). Затем ход переходит к сопернику. Одинаковые слова не допускаются. Если игрок не в состоянии придумать очередное слово (это относится как к человеку, так и к компьютеру), он может пропустить ход.

Разберём для примера типичное начало игры (рис. 4.13). Исходное слово ( ВЫВОД ) записывается в середине поля. Первый игрок добавляет букву О, тем самым образуя слово ОВОД (C2-C3-D3-E3). Второй игрок выкладывает на поле букву А, подразумевая слово ВОДА (C3-D3-E3-E4).

С++ мастер-класс. 85 нетривиальных проектов, решений и задач

В строке, помеченной звёздочкой, мы знаем позицию текущей клетки, текущую просматриваемую букву и список корректных слов, соответствующих данному варианту хода. Остаётся лищь выбрать ход, которому соответствует самое длинное слово.

Несколько неочевидной может быть процедура получения всех цепочек клеток, включающих данную. Здесь опять используется переборный алгоритм: начиная от текущей клетки нужно рекурсивно изучить каждую дорожку , начинающуюся сверху, слева, снизу и справа от текущей. Изучение очередной дорожки заканчивается либо в случае самопересечения, либо при выходе за пределы уже заполненных буквами клеток. Обратите внимание, что размещаемая игроком буква не обязана начинать или заканчивать слово, поэтому дорожка может продолжаться в две стороны от текущей клетки.

Программа, прямолинейно реализующая приведённый псевдокод окажется очень медленной. Не хочу цас лишать удовольствия самостоятельно провести оптимизацию, но некоторые идеи лежат на поверхности. Например, можно попробовать сразу построить все находящиеся на игровом поле цепочки клеток, в которых не хватает одной буквы до полноценного слова. Далее с помощью словаря игры находится подходящее слово и, следовательно, буква, размещаемая на данном ходе.

4.2.4. Пентамино, или ещё одна задача на перебор с возвратами

С клавиатуры вводятся числа М и N. Требуется определить, можно ли полностью замостить прямоугольник NxM фигурами пентамино (рис. 4.14).

При решении можно использовать либо все 12 фигур, либо меньшее количество, но не допускается класть на доску одну и ту же фигуру дважды. При установке на поле фигуры пентамино разрешается поворачивать и переворачивать лицевой стороной вниз (при этом получится зеркальное отражение).

Компьютер должен выдавать решение (например, выводить прямоугольник, в котором различные фигзфы закрашены разными цветами) либо печатать сообщение о том, что решения не существует.

Рис 4.14. Набор фигур пентамино

4.2.5. Кубики сома - трёхмерный аналог полимино

Кубики сома - это трёхмерный аналог фигур полимино. Полный набор кубиков сома состоит из семи фигур (одна из них составлена из трёх единичных кубиков, остальные шесть - из четырёх) и представлен на рис. 4.15. Переформулировка предыдущей задачи для кубиков сома звучит так: составить из всех семи кубиков куб размером 3x3. Я предлагаю рассмотреть, общий случай составления заданной трёхмерной фигуры из семи кубиков сома.

Во входном файле хранится описание составляемой фигуры. Пожалуй, проще всего это сделать с помощью списка прямоугольных матриц, состоящих из нулей и единиц. Каждая матрица задаёт вид очередного слоя фигуры (от нижнего к верхнему).

Программа находит решение (в отличие от предыдущей задачи требуется использовать все кубики) и выводит построенную фигуру на экран. Можно для наглядности изобразить её с нескольких сторон. Отдельные кубики сома выделяются разными цветами.

Для затравки можно попытаться построить фигуры из книги Мартина Гарднера Математические головоломки и развлечения (Москва, Мир , 1999 г.) (рис. 4.16).

Так, Авианосец задаётся набором < матриц:

111111111 111111111

001111100 000000000

000111000 000000000

000010000 000000000

Рис 4.15. Набор кубиков сома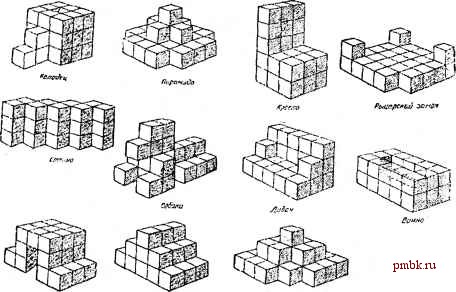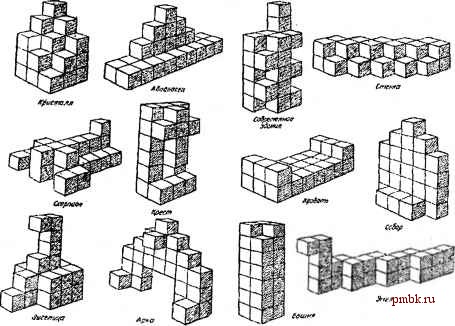

Рис 4.16. Фигуры для сборки из кубиков сома

Рис 4.17. Составление слова ИГРА из костей домино

4.2.7. Людоеды и миссионеры Поиск решения известной головоломки

Написать программу, решающую классическую головоломку людоеды и миссионеры .

На одном из берегов реки находятся три людоеда и три миссионера. Их задача - переправиться на другой берег В распоряжении у компании имеется лишь одна двухместная лодка, поэтому придётся совершить несколько рейдов на другой берег и назад. Обратите внимание, что на двухместной лодке можрю перевезти как двух, так и одного человека.

Задача усложняется ещё одним не очень приятным фактом: если количество людоедов на одном из берегов в какой-то момент времени превысит количество миссионеров, миссионеры будут немедленно съедены, чего допустить никак нельзя.

Программа должна печатать последовательность перевозок, обеспечивающую безопасную переправу.

4.2.6. Головоломка с домино - несколько более сложный случай перебора

Эту задачу я позаимствовал из книги Л.П. Мочалова Головоломки: Книга для учащихся (Москва, Просвещение , 1996 г.)

Требуется выстроить слово ИГРА (рис. 4.17) из всех 28 костей домино таким образом, чтобы на соприкасающихся половинках костей были написаны одинаковые числа (то есть по обычным правилам игры). Количество очков на каждой из букв должно быть одним и тем же.