Koch(order - 1, XI, Yl, Xa, Ya)

Koch(order - 1, Xa, Ya, Xc, Yc)

Koch(order - 1, Xc, Yc, Xb, Yb)

Koch(order - 1, Xb, Yb, X2, Y2)

Построить кривую N-го порядка теперь можно с помощью вызова:

Koch(N, MainForm->PaintSurface->Width / 4,

2*MainFonn->PaintSurface->Height / 3, 3*MainFonn->PaintSurface->Width / 4, 2*MainFonn->PaintSurface->Height / 3);

Треугольник Серпинского немного сложнее графически, но проще математически. В чертеже треугольника со стороной len, нижний левый угол которого находится в точке (х, у), нам потребуется знать координаты ещё пяти точек (рис. 4.7).

X + \€п12. у - Icii * sqrf(3)/2

Глава 4. Рекурсия и перебор с возвратами. Эвристический поиск Следуя традиции, приведу сначала процедуру на псевдокоде: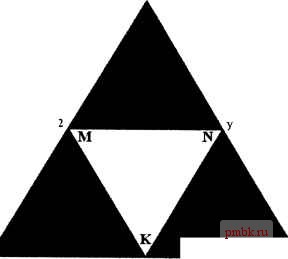

X + 1еа/4. y-len*sci1(3)/

х + 3*1еп/4. -len*scirt(3)/2

X, у X + 1еп/2, у X + len. у

Рис 4.7. Базовый злемент треуголы1ика Серпинского

построить чёрный треугольник ABC A.f

ЕСЛИ order (порядок треугольника) бсяйЛе нуля], построить белый треухольник ШК1 * 4*

построить треугольники Серпинского т фящка ordrr tco стороной len/2 в точках А, м и К ЦШ г

Следующая функция реализует приведенный алгоритм на С++:

void Sierpinski(int order, int x, int y, int len) {

const double s3d2 = sqrt(3) / 2;

TCanvas *p = MainForm->PaintSurface->Canvas;

построить чёрный треугольник ABC p->Pen->Color = clBlack; p->Brush->Color = clBlck; p->MoveTo(X, у);

p->LineTo(x + len/2, у - len * s3d2); p->LineTo(x + len, y); p->LineTo(x, y);

p->FloodFill(x + len/2, у - 1, clBlack, fsBorder);

if(order > 0) {

построить треугольник MNK

p->Pen->Color = clWhite;

p->Brush->Color = clWhite;

p->MoveTo(x + len/2, y);

p->LineTo(x + len/4, у - len * s3d2/2);

p->LineTo(x + 3 * len/4, у - len * s3d2/2);

p->LineTo(x + len/2, y);

p->FloodFill(x + len/2, у - 1, clWhite, fsBorder);

построить треугольники порядка order - 1 Sierpinski(order - 1, x, y, len / 2); Sierpinski(order - 1, x + len/2, y, len/2); Sierpinski(order - 1, x + len/4, у - len * s3d2/2, len/2);

Для построения тре)ольника N-го порядка следует выполнить вызов:

sierpinski(N, MainForm->PaintSurface->Width / 4,

2*MainForm->PaintSurface->Height /3, MainForm->PaintSurface->Width / 2);

double Xb = XI + 2 * R * cos(alpha) / 3, Yb = Yl + 2 * R * sin(alpha) / 3;

Рс <

Рис 4.8. Построение драконовой ломаной

При увеличении порядка ломаной каждый сегмент заменяется двумя отрезками, расположенными под прямым углом. Первая пара отрезков находится слева от сегмента ломаной предыдущего порядка, вторая - справа, третья снова слева и так далее.

Построение ломаной удобно разбить на две функции. Первая возврап1ает массив точек, соответствующих углам ломаной:

vector<TPoint> GetDragonPolyline(int order);

Вторая (главная) запрашивает ломаную в виде массива точек и выводит её на экран:

void Dragon(int order) {

vector<TPoint> line = GetDragonPolyline(order);

MainFonn->PaintSurface->Canvas->MoveTo(line[0].x, line[0].y); for (unsigned i = 1; i < line.sizeO; i + +)

MainForm->PaintSurface->Canvas->LineTo(line[i].x, line[i].y);

Алгоритму фзшкции GetDragonPolyline () запись на псевдокоде не добавит понятности, поэтому я сразу приведу окончательный код функции:

vector<TPoint> GetDragonPolyline(int order) {

return line;

4 Зек. 772

if(order == 0) {

ломаная нулевого порядка состоит из одного сегмента

vector<TPoint> line;

добавить первую и последнюю точки

line.push back(TPoint(MainFonn->PaintSurface->Width/4,

MainFonn->PaintSurface->Height/2));

line.push back(TPoint(3*MainFonn->PaintSurface->Width/4,

MainFonn->PaintSurface->Height/2));

return line;

получить ломаную предыдущего порядка

vector<TPoint> prevline = GetDragonPolyline(order -1);

vector<TPoint> litie;

знак направления угла (1 - влево, -1 - вправо) int DirSign = 1;

начальная точка ломаной не изменяется line.push back(prevline[0]);

for(unsigned i = 0; i < prevline.size() - 1; i++) {

считать очередной сегмент ломаной TPoint pi = prevline[i]; TPoint p2 =.prevline[i + 1];

double alpha = atan2(p2.y - pl.y, p2.x - pl.x) -

DirSign * M PI / 4; double R = sqrt((pl.x - p2.x)*(pl.x - p2.x) +

(pl.y - p2.y)*(pl.y - p2.y)) / sqrt(2);

найти новую точку ломаной (рс)

TPoint рс(р1.х + R*cos(alpha), pl.y + R*sin(alpha));

добавить рс и p2 в список точек текущей ломаной line.push back(рс); line.push back(p2);

изменить направление на противоположное DirSign = -DirSign;

Начертить драконову ломанзто, пожалуй, несколько труднее. Для начала рассмотрим, каким образом драконова ломаная N-ro порядка строится на основании ломаной порядка N-1 (рис. 4.8).

4.2.1. Генератор кроссвордов

Знакомство с перебором с возвратами

В текстовом файле crossword.txt задана конфигурация кроссворда в следующем формате:

ШИРИНА ВЫСОТА

XI Y1 ДЛИНА1 НАПРАВЛЕНИЕ!

Х2 Y2 ДЛИНА2 НАПРАВЛЕНИЕ2

XN YN ДЛИНАЫ HAПPABЛEHИEN

Пара координат (Хк, Yk) указывает расположение слова в сетке кроссворда. Параметр ДЛИНА задаёт длину, а НАПРАВЛЕНИЕ - направление слова (v - вертикальное, сверху вниз; h - горизонтальное, слева направо). Например, файл

13 4

2 О 4 V

0 1 8 1

1 3 7 3

задаёт кроссворд, изображённый на рис. 4.9.

Рис. 4.9. Пример кроссворда

Второй файл vocabulary.txt содержит словарь, то есть список разрешённых для использования в кроссвордах слов. Программа должна выдать возможное решение кроссворда с использованием слов словаря либо сообщение о том, что решения не существует.

Если теперь вызвать функцию Solve () для самой первой (то есть нулевой) позиции, мы получим полное решение кроссворда.

Рассмотрим устройство этой функции подробнее; Позиция К = N соответствует полностью заполненному кроссворду, поэтому функции остаётся лишь вернуть значение true (успех).

Если же текущая позиция подлежит заполнению, алгоритм просматривает все незанятые слова словаря в поисках подходящей кандидатуры. Если очередное слово можно разместить на текущей позиции (то есть оно подходит по длине и не противоречит уже вписашым буквам), то алгоритм вписывает слово в кроссворд и вызывает функцию решения подкроссворда , начинающегося с позиции К + 1. Если подкроссворд репшть не удаётся (Solve (К + 1) возвращает false), алгоритм пытается выбрать другое подходящее слово для вписывания в позицию К.

Займёмся теперь реализацией программы. Для начала нам потребуются структ)фы, описывающие отдельные буквы, вписываемые в кроссворд, и слова словаря:

буква со счётчиком struct CharAndCounter {

char Char;

Решение

Эта задача хорошо иллюстрирует методику перебора с возвратами. Допустим, в кроссворде предусмотрено N позиций, предназначенных для вписывания слов (таким образом, решённый кроссворд будет состоять из N слов). Решение кроссворда сводится к вписыванию некоторого слова в первую свободную позицию и решению подкроссворда из N - 1 позиций. Центральное место в алгоритме решения занимает функция Solve (К), заполняющая подкроссворд начиная с позиции К:

bcjoi Solvetm&igned к) %

корректны лить позиции 0...N-1

ЕСЛИ К = N, return true s - ,

ЦИКЛ подвеем пъшущjfbOi&jKisi чк1Г -

ЕСДЙ очередное jtijiofeq моашо %амсташ <~111ко(Ырт11с. \ , разместить W позиции К - \ . .i\J\ty ЕСЛИ Solve (К + i) = true, retH3r*ji €гив \

снять слово W с ПОЗИ1ЦШ Кч

КОНЕЦ ЦИКЛА return feXse

4.2. ПРОСТОЙ ПОИСК В ИГРАХ И ГОЛОВОЛОМКАХ