ГЛАВА 4. РЕКУРСИЯ И ПЕРЕБОР С ВОЗВРАТАМИ. ЭВРИСТИЧЕСКИЙ ПОИСК

Заметьте, что эту задачу можно решить, моделируя растекание жидкости по всей фигуре из начальной точки, то есть пользуясь уже рассмотренньп! алгоритмом волновой трассировки (см. п. 3.2.1. Волновая трассировка ).

Если задачу не удаётся решить, скажем так, научным методом, остаётся лишь воспользоваться перебором вариантов, ибо как известно, полный перебор всегда находит решение задачи. Организащ1Я перебора при этом вовсе не является технической формальностью. Как правило, в большинстве задач приходится использовать нетривиальные рекурсивные алгоритмы поиска, да ещё и в сочетании со специальными оптимизациями (в противном случае алгоритм будет работать недопустимо медленно). Иногда скорость поиска можно повысить за счёт использования эвристических алгоритмов.

Данная глава начинается с разминочной задачи, посвященной рекурсивным объектам. Потренировавшись в сочинении рекурсивных процедур, мы перейдём к алгоритмам перебора с возвратами (различного уровня сложности). Глава завершается изучением процедуры эвристического поиска А*.

4.1. РЕКУРСИВНЫЕ ОБЪЕКТЫ. ФРАКТАЛЬНЫЕ УЗОРЫ

Рисование реюфсивных объектов

По неформальному определению основоположника фрактальной геометрии Бенуа Мандельброта, фрактал - это структура, состоящая из частей, которые в каком-то смысле подобны целому . Такие самоподобные объекты нередко встречаются в природе. К ним относятся растения (ветка куста в каком-то смысле подобна всему кусту), морские волны, облака. Задав небольшой набор параметров фрактала, можно получить очень живописный, реалистичный рисунок. На практике фракталами действительно польззтотся при моделировании пейзажей (например, для компьютерных мультфильмов). Возможно, вам также встречались в интернете галереи диковинных, поразительно сложных и красивых фрактальных узоров.

Существует Множество приложенийдля работы с фрактальными объектами. Разработаны методики описания фракталов, такие как системы Лин-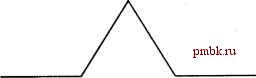

Рис 4.1. Кривая Коха первого порядка

Рис 4.2. Кривая Коха второго порядка

Салфетка Серпинского нулевого порядка состоит из закрашенного равностороннего треугольника (цветом закраски считается чёрный). Салфетка первого порядка получится, если разделить треугольник на четыре равные части и извлечь центральную (то есть снять с неё закраску, рис. 4.3). При повторении процесса для оставшихся закрашенными частей треугольника образуется салфетка второго порядка (рис. 4.4) и так далее.

денмайера (L-системы). Мы остановимся лишь на самых простых примерах фракталов, когда связь между частями и целым очень проста.

Рассматриваемая задача заключается в рисовании на экране трёх различных фрактальных объектов К-го порядка (значение К вводится с клавиатуры) - кривой Коха, салфетки Серпинского и драконовой ломаной.

Кривая Коха нулевого порядка представляет собой обыкновенный отрезок. Для получения кривой первого порядка отрезок делится на три равные части, и средний интервал заменяется отрезками, длина каждого из которых равна трети длины исходного отрезка (рис. 4.1). Чтобы получить кривую второго порядка, следует повторить процесс для каждого из четырёх полученных отрезков (рис. 4.2). Повторяя алгоритм, можно сгенерировать кривую Коха любого требуемого порядка.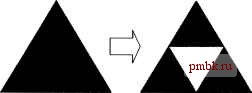

Рис 4.3. Салфетка Серпинского первого порядка

Драконова ломаная К-го порядка получится, если согнуть полоску бумаги пополам К раз (сгиб всегда производится в одну и ту же сторону), а потом разогнуть так, чтобы каждый угол сгиба был равен 90 градусам (рис. 4.5). Можно определить драконову ломаную и рекурсивно (подумайте как).

Рис 4.4. Салфетка Серпинского второго порядка

Решение

Рис 4.5. Драконова ломаная второго порядка

Поскольку эта задача требует графических построений, придётся выйти за рамки стандартного С++ и воспользоваться возможностями библиотеки VCL, входящей в состав Borland C++Builder. Предположим, что главна форма приложения называется Main Form, а на ней расположен объект PaintSurf асе типа TImage.

Xc,Yc

Xb.Yb

XI. Yl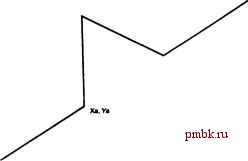

X2.Y2

Для того чтобы постро-HTbKpHBjno Коха,необхо-димо научиться чертить приведённую на рис. 4.6 фигуру для любых данных точек (XI, Y1) и (Х2, Y2).

Рис.4.6. Базовый злемент кривой Коха

Глава 4. Рекурсия и перебор с возвратами. Эвристический поиск Точки (Ха, Ya), (Xb, Yb) и (Хс, Yc) определяются по формулам:

а=гШ2(У2-П,Х2-Х\) R = yl{X2-Xlf + {Y2-YlY

Ха = Xl-t-jCOs(a),yfl =yi + ysin(a)

Xb = Xl -f- cos(a), УЬ = 71 -н -у sin(a)

Хс = Xa -ь у cos(a -у), Yc=Ya -t- у sin(a -у)

Напомню, что функция atan2 (у, х) возвращает угол между осью абсцисс и отрезком, соединяющим начало координат с точкой (х, у).

На псевдокоде алгоритм построения кривой Коха порядка order на отрезке (XI, Y1, Х2, Y2) выглядит следующим образом:

ЕСЛИ охбец *С просто построят <уфвзок (Xli УХ, Х2, У?) /-;>

ИНАЧЕ - / i /

\ построить крьшую Коха порзадкаvoider - 1 на озрезке {XI,. YU Ха, Yk\J

* й-ь ривую Коха порядка odl, Щ.ЩйР

**-1фйую,Коха порядкаЛЙН# Щ ЩШЩ

Соответствующий код на С++ абсолютно прямолинеен:

void Koch(int order, int Xl, int Yl, int X2, int Y2) {

if(order == 0) {

построить отрезок (Xl, Yl) - (X2, Y2) MainForm->PaintSurface->Canvas->MoveTo(Xl, Yl) ; MainForm->PaintSurface->Canvas->LineTo(X2, Y2);

else {

double alpha = atan2 (Y2 - Yl, X2 - Xl). ;

double R = sqrt((X2 - Xl)*{X2 - Xl)+(Y2 - Y1)*{Y2 - Yl));

вычислить значения Xa, Ya, Xb, Yb, Xc, Yc double Xa = XI + R * cos(alpha) / 3,

Ya = Yl + R * sin(alpha) / 3; double Xc = Xa + R * cos(alpha - M PI / 3)/3,

Yc = Ya + R * sin(alpha - M PI / 3)/3;