Рассмотрим в качестве примера простую коллекцию страниц: l.html

содержит строку href= /2.html * 3 . html

содержит строку href= /2.html 4.html

содержит строки href = /5 .html *, href= /6 .html и href=-/7.html

2.html, 5.html, 6.html, 7.html не содержат никаких ссылок

Программа разобьёт коллекцию на два кластера. В первом окажутся документы Lhtml, 2.html и 3.html, во втором - 4.html, S.html, 6.html и 7.htnil.

3.2. ВОЛНОВАЯ ТРАССИРОВКА 3.2.1. Волновая трассировка

Поиск маршрута в лабиринте

Имеется лабиринт, заданный прямоугольной матрицей из нулей и единиц. Нуль означает стену, единица - проход (рис. 3.2). Разумеется, крайние строки и столбцы матрицы будут состоять полностью из нулей (чтобы не выйти из лабиринта в никуда ). Матрица считывается из файла.

Задача состоит в том, чтобы автоматически построить кратчайший маршрут между входом и выходом. Стартовой локацией лабиринта (читается верхний левый угол, финишной - нижний правый. Лабиринт требуется отобразить на экране в виде плоской карты, отметив найденный маршрут ломаной красного цвета.

0 0 00000000 0111001110 0001111000 0111001110 0000000000

Рис. 3.2. Представление лабиринта с помощью текстового файла

Существует несколько известных алгоритмов поиска пути в лабиринтах. В этой задаче предлагается воспользоваться так называемым методом волновой трассировки. Его можно описать, например, как моделирование поведения растекающейся воды.

Представьте, что в стартовой локации лабиринта опрокинули бак с водой. Вода растекается во все доступные стороны, заполняя на очередной итерации моделирования все локации, граничащие с уже затопленными, пока выход из лабиринта не будет достигнут. Если на очередном шаге не удалось затопить ни одной новой локации, это означает, что решения не существует (то есть путь к выходу огорожен глухой стеной). Затем программа отслеживает, каким путём вода попала в финишную локацию, и строит маршрут. Найденный таким образом маршрут и окажется кратчайшим.

Решение

Думаю, решение этой задачи вполне достаточно привести на псевдокоде. Все промежуточные операции будут выполняться в служебном двумерном целочисленном массиве, размеры которого совпадают с размерами лабиринта.

Изначально элемент массива, соответствующий стартовой локации лабиринта, равен единице. Все остальные элементы равны нулю. Далее выполняются действия:

N = 1 .

ЦИКЛ . . Ij

ДЛЯ КАЖДОГО элемента массива, равного N - -

ЕСЛИ текущему элементу массива соответствует финишная, .локация: решение найдено; конец алгоритма - ДЛЯ КАЖДОГО: элемента, соседнеЕО; .С-.:-.2текущим Щ50вери№

1) равен ли он нулю -<

2) есть ли стена между двумя локациями,..со С:;СЛвующ1миг:,;; рассматриваемым элементам массива

.ЕСЛИ оба условия выполнены ,

присвоить.соседнему элементу значение N + 1

КОНЕЦ ЦИКЛА

::CharToOem( Перекластеризуем граф: \п-, buf ); cout buf endl; GetClusters(); ShowGraph(); SaveGraph{);

getch(); return 0;

f ЕСЛИ ш ОДНО значение N +,Гнё было присвоено решения не существует; конец гшгоритма

КОНЕЦ ийКЛХ>; . -

Первые три итерации алгоритма иллюстрирует рис. 3.3. В нашем примере при N = 8 алгоритм завершит работу (рис. 3.4).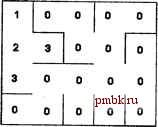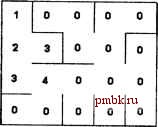

Рис. 3.3. Работа алгоритма волновой трассировки

Рис. 3.4. Результат работы алгоритма волновой трассировки

Теперь осталось восстановить путь от стартовой локации до финишной. Сделать это несложно: в финишную локацию (которой соответствует число N) мы попали из той соседней с ней локации, которой соответствует число N - 1; в свою очередь, в нее можно попасть из локации N - 2 и так далее до стартовой локации. Разумеется, на каждом шаге необходимо следить, чтобы движение осуществлялось по свободному проходу, а не сквозь стену.

3.2.2. Цветные линии

Волновая трассировка в популярной игре

В Цветные линии (Color lines) будут играть и тогда, когда третий Doom станет антикварной редкостью, пылящейся на дальнем стеллаже коллекционера. Наверное, в рейтинге проектов, через которые проходит каждый программист, цветные линии попадут если не в первую десятку, то в первую двадцатку точно. Сейчас я предлагаю вам написать свою версию этой замечательной игры.

Процесс игры достаточно прост. На клетчатой доске размером 9x9 появляется три цветных шарика (цвета выбираются случайно из палитры в 6 цветов, рис. 3.5). Игрок может переместить любой шарик в любую доступную клетку (доступность определяется возможностью построить путь к ней от текущей клетки, перемещаясь по свободным клеткам в горизонтальном и вертикальном направлении).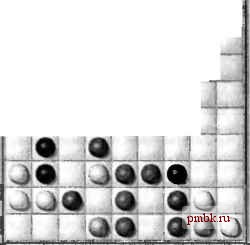

Рис. 3.5. Игра Color lines

Волновая трассировка плюс немного фантазии

В Square Head играют на прямоугольном поле размером 32x20 клеток. В начальный момент клетки раскрашены случайными цветами (в палитре игры всего семь цветов). Первому игроку принадлежит верхний левый угол поля, второму - правый нижний. Очередным ходом игрок перекрашивает свою угловзто клетку в какой-либо новый цвет. В результате перекрашивается вся область клеток цвета игрока, примыкающих к угловой клетке. Иначе го* воря, клетка перекрашивается, если до неё можно дойти из угловой клетки по клеткам одного цвета (ходить можно лишь вправо, влево, вверх и вниз).

На рис. 3.6 показано перекрашивание левого верхнего угла (то есть области первого игрока) из белого в серый цвет.

Рис. 3.6. Square Head: ход первого игрока

Совершая ход, нельзя выбирать в качестве нового цвета области свой текущий цвет, а также текущий цвет противника.

Как видно из рисунка, при перекрашивании область игрока расширяется (происходит захват соседних клеток). Игра заканчивается, как только всё поле будет раскрашено в два цвета, принацлежащие игрокам. Победителем объявляется тот игрок, чья область насчитывает больше клеток.

Задача заключается в реализации игры Square Head. В программе должны быть предусмотрены режимы игры между двумя людьми и между человеком и компьютером (разумеется, для компьютера придётся придумать разумную стратегию).

Подсказка

Конечно, Square Head не шахматы, но даже здесь изобрести идеальную процедуру игры не так просто. Здесь я могу лишь предложить несколько разумных соображений.

Даже простой жацный алгоритм (на очередном ходе выбрать цвет, приводящий к наибольшему расширению области игрока) работает достаточно хорошо. Для оценки прироста области можно использовать уже знакомый вам алгоритм волновой трассировки.

Можно попробовать не только максимизировать свой выигрыш, но и минимизировать выигрыш оппонента. Предположим, что наибольший прирост области (+10 клеток) даёт выбор красного цвета. При этом соперник выбирает синий цвет и добавляет к своей области, допустим, 15 клеток. Если же мы во время своего хода выберем синий, сопернику придётся довольствоваться каким-нибудь другим ходом. Таким образом, признаком лучшего хода будет не максимальная величина прироста своей области, а максимальное значение разности ПриростСвоейОбласти - ПриростОбластиСоперника

Можно представить одиночную партию в Square Head как серию мини-игр , состоящих из трёх-четырёх ходов. Цель каждой мини-игры - максимальное расширение своей области (иными словами, речь идёт об анализе на глубину в 3-4 хода). Такая программа ещё не будет слишком медленной, но сила её игры определённо возрастёт. Конечно, известная в шахматах проблема горизонта присутствует и здесь, но, как мне кажется, её значение в данном случае не очень велико.

3.2.4. Закраска контура, или необычное применение волновой трассировки

Требуется написать процедуру закраски произвольного замкнутого контура (начальная точка, откуда начинается закраска, передаётся процедуре).

9 Когда программа пропускает серьёзную атаку соперника, поскольку фиксированная глубина

просмотра не позволяет её заметить.

После каждого хода в свободных ячейках поля появляются три новых шарика. Цель игрока - собрать вертикальную, горизонтальную или диагональную линию из пяти или более шариков. Собранная линия уничтожается, а игрок получает призовые очки. Если поле оказывается заполненным до отказа, это означает конец игры.

Подсказка

Для построения маршрута движения шарика по игровому полю воспользуйтесь алгоритмом волновой трассировки (см. п. 3.2.1).

3.2.3. Игра Square Head