vector<int> v;

for (int k=0; k<7; k++) v.push back(10 * k);

Содержимое v: 0, 10, 20, 30, 40, 50, 60 v.erase(v.begin()+2, v.begin()+5);

Содержимое v: 0, 10, 50, 60

Обе функции erase занимают время 0(n), где n - число элементов, которые следуют за удаляемыми элементами. Если нам нужно удалить несколько последовательных элементов вектора, мы должны использовать один вызов последней функции erase, поскольку это значительно быстрее, чем несколько раз вызывать предпоследнюю функцию, которая удаляет по одному элементу за раз.

3.4. Двусторонние очереди

Различные типы контейнеров очень похожи в отношении способов их применения. Например, каждый из трех типов контейнеров (vector, deque и list) определяет конструктор, который использует в качестве параметров число повторений и значение, например:

vector<double> v(100, 12.34); deque<double> D(100, 12.34); list<double> L(100, 12.34);

Каждое из этих объявлений создает последовательность, состоящую из 100 экземпляров значения 12.34. Из примера следует, что можно сократить наше обсуждение двусторонних очередей и списков, ограничившись рассмотрением специфических свойств этих контейнеров и делая ссылку на векторы относительно общих аспектов.

Наше обсуждение двусторонних очередей в разделах 1.3 и 1.9 позволяло сделать вывод, что эти структуры данных обладают только преимуществами перед векторами. Кроме функций-членов, определенных для векторов, они определяют функции-члены push Jront и pop Jront. Так как одна из существенных характеристик двусторонней очереди - это возможность расти и сокращаться с двух сторон, кажется естественным реализовать двустороннюю очередь с помощью двусвязного списка. Однако в STL двусторонняя очередь реализована по-другому, поскольку, что удивительно, двусторонняя очередь в STL обеспечивает произвольный доступ к элементам за постоянное время. На чем основана такая реализация? Рисунок 3.2 дает набросок модели реализации. Элементы двусторонней очереди размещаются в блоках фиксированного размера. Кроме этого, хранится массив указателей на эти блоки. Заштрихованные области блоков действительно используются контейнером, а белые области означают выделенную, но неиспользуемую память.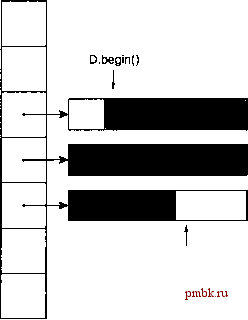

D.endO

Рисунок 3.2. Возможная реализация двусторонней очереди D

Выполнение

D.push front(х);

предполагает, что элемент х помещается слева от позиции, обозначенной D.begin(). Эта вставка в начале D заставляет первую стрелку i сместиться влево. После того как эта операция выполнится несколько раз, первый из блоков, изображенных на рисунке, станет заполненным. Тогда будет размещен новый блок, указатель на который будет помещен в позицию 1 массива, изображенного слева. Когда и этот блок заполнится, будет выделен следующий блок, указатель на который займет место в позиции О массива. Может показаться, что должна возникнзггь проблема, когда после нескольких дополнительных вставок и этот блок также заполнится. Однако с этой проблемой можно справиться с достаточной эффективностью, перераспределив память для массива указателей. Когда у нас появятся пять блоков, мы вьщелим память под больший массив указателей, в котором будут использоваться только пять элементов в середине, что даст возможность снова расширять структуру с обоих концов. Легко видеть, что вставка в конце (а не в начале) работает по сходным механизмам.

void push front(const T& x); void pop front(); reference front();

Например, предположим, у нас имеются вектор v и двусторонняя очередь D, оба непустые и хранящие элементы одного и того же типа. Тогда следующий фрагмент заменяет последний элемент v первым элементом D, после чего первый элемент D стирается:

v.backO = D. front О ; D.pop front();

3.5. Списки

Как известно, преимущество списков перед векторами и двусторонними очередями заключается в том, что вставка и удаление элементов в любой

Не существует гарантий, что после вставки элементов итераторы, которые ссылаются на двусторонние очереди, останутся действительными. Напомним, что это утверждение справедливо и для векторов, как мы видели в разделе 3.2. Так как все блоки на рисунке 3.2 обладают одинаковой длиной, адрес элемента двусторонней очереди может быть вычислен за постоянное время; другими словами, двусторонние очереди предоставляют произвольный доступ к своим элементам. Мы даже можем использовать применяемую для массивов запись

D[k] вместо * (D.beginO + к)

Учитывая более сложную схему распределения памяти, можно ожидать, что операции с двусторонними очередями будут выполняться несколько медленнее, чем операции с векторами. Это объясняет логику, по которой в STL имеются обе эти структуры: функции pus/z Jront и pop Jront, выполняющиеся за постоянное время, доступны для двусторонних очередей, но не для векторов, но большинство тех операций, которые определены для обоих контейнеров, вероятно, будут выполняться несколько быстрее для векторов по сравнению с двусторонними очередями.

Для двусторонних очередей не определены функции reserve и capacity (см. раздел 3.2), но есть функция-член size, и, как обычно,

D.sizeO эквивалентно D.end - D.beginO

Большинство функций двусторонних очередей ведут себя так же, как их аналоги для векторов (см. раздел 3.3). Вот несколько объявлений функций-членов класса deque, которые отсутствуют в классе vector.