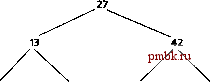б 17 33 48

Рис. 15.18. Дерево двоичного поиска

Дерево двоичного поиска упрощает процесс удаления дубликатов. Если дерево создано, попытка поместить в него дублирующее значение будет распознана при каждом решении следовать налево или следовать направо . Значение дубликата в этот момент может просто отбрасываться.

Процесс поиска значения в бинарном дереве, соответствующего некоторому ключевому значению, также является быстрым. Если дерево является плотно упакованным, то каждый уровень содержит примерно вдвое больше элементов, чем предыдущий уровень. Таким образом, дерево двоичного поиска СП - элементами имеет максимум log2n уровней и, таким образом, для того, чтобы найти соответствующее значение или убедиться, что его нет, требуется произвести максимум log2n сравнений. Это означает, например, что при проведении поиска в плотно упакованном дереве, содержащем 1000 элементов, требуется провести не более 10 сравнений, поскольку 2° > 1000. При поиске в плотно упакованном дереве, содержащем 1 ООО ООО элементов, требуется провести не более 20 сравнений, поскольку 2 > 1 ООО ООО.

В упражнениях представлены алгоритмы для проведения некоторых операций с бинарным деревом, а именно: удаление элемента из дерева, печать дерева в двумерном формате и послойный обход дерева. Послойный обход дерева подразумевает его просмотр по уровням, начиная с корневого узла. На каждом уровне дерева обход производится слева направо. Другие упражнения с бинарным деревом позволяют ему хранить дублирующие значения, вставлять в дерево строки и определять количество уровней в дереве.

Резюме

Классы с самоадресацией содержат элементы, называемые указателями связи, которые, в свою очередь, указывают на объекты того же класса.

Классы с самоадресацией позволяют объединять объекты класса в стеки, очереди, списки и деревья.

Динамическое выделение памяти резервирует во время выполнения программы блок байтов в памяти для хранения объекта.

Связный список является линейной набором объектов класса с самоадресацией.

Связный список является динамической структурой данных - длина списка может увеличиваться или уменьшаться по мере необходимости.

Размер связных списков может наращиваться до тех пор, пока не исчерпана память.

Связные списки обеспечивают простые механизмы вставки и удаления данных путем манипулирования указателями.

Стеки и очереди являются частным случаем связных списков.

Новые узлы стека добавляются в него или удаляются только на вершине стека. По этой причине стек относится к структурам данных типа последним вошел - первым вышел ( last-in, first-out - LIFO).

Элемент указатель связи последнего узла списка устанавливается в нуль для того, чтобы обозначить дно стека.

Двумя основными операциями, которые используются для управления стеком, являются push и pop. Операция push создает новый узел и помеш;ает его в вершину стека. Операция pop удаляет (выталкивает) узел из вершины стека, освобождает выделенную для него память и возвраш;ает удаленное значение.

В структуре данных очередь узлы удаляются из головы (начала) очереди и добавляются в ее хвост (в конец). По этой причине очередь относится к структурам данных типа первым вошел - первым вышел ( first-in, first-out - FIFO). Операции добавления в очередь и удаления из нее известны как enqueu и dequeue.

Деревья являются двумерными структурами данных, требуюпцими два или более указателей связи на узел.

Бинарные деревья имеют два указателя связи в каждом узле.

Корневой узел является первым узлом дерева.

Каждый из указателей в корневом узле обращается к узлу-потомку (дочернему узлу). Левый узел-потомок является первым узлом левого поддерева, а правый узел-потомок является первым узлом правого поддерева. Порожденные одним каким-либо узлом узлы-потомки называются родственными узлами или узлами-братьями. Любой узел дерева, который не имеет каких-либо узлов-потомков, называется листом дерева или концевым узлом.

Дерево двоичного поиска характеризуется тем, что значение в левом узле-потомке меньше значения в его родительском узле, а значение в правом узле-потомке больше или равно значению в его родительском узле. Если нет дублирующих значений, то значение в правом узле-потомке просто больше значения в его родительском узле.

При последовательном (симметричном) обходе двоичного дерева проводится последовательный поиск в левом поддереве, обрабатывается значение в корневом узле, а затем проводится последовательный поиск в правом поддереве. Значение в узле не обрабатывается до тех пор, пока не закончится обработка значений в его левом поддереве.

При обходе в ширину (прямом обходе) обрабатывается значение в корневом узле, проводится поиск в ширину в левом дереве, а затем проводится аналогичный поиск в правом поддереве. Значение в каждом узле обрабатывается, как только этот узел встречается при выполнении обхода.

При обратном обходе проводится обратный обход в левом поддереве, затем проводится обратный обход в правом поддереве, а затем обрабатывается значение в корневом узле. Значение в каждом узле не обрабатывается до тех пор, пока не будз обработаны значения в обоих его поддеревьях.

Терминология

dequeue enqueue

FIFO ( первым вошел -

первым вышел LIFO ( последним вошел -

первым вышел ) pop push sizeof

бинарное дерево

вершина

вставка узла

голова очереди

двойное разименовывание

дерево

дерево двоичного поиска динамические структуры данных динамическое выделение памяти дочерний узел концевой узел корневой узел левое поддерево левый узел-потомок линейная структура данных лист дерева

нелинейная структура данных

нулевой указатель обратный обход обход

обход в ширину (прямой обход)

очередь

поддерево

посещение узла

последовательный (симметричный) обход

послойный обход бинарного дерева

правое поддерево

правый узел-потомок

родительский узел

родственные узлы

связный список

сортировка бинарного дерева

стек

структура с самоадресацией удаление дубликатов удаление узла узел

узлы-потомки указатель на указатель функция предикат хвост очереди

Типичные ошибки программирования

15.1. Указатель связи в последнем узле не устанавливается на нуль (О).

15.2. Предположение о том, что размер объекта класса является простой суммой размеров его данных-элементов.

15.3. Не осуществляется возвращение динамически выделенной памяти, когда эта память уже более не требуется. Это может явится причиной преждевременного переполнения памяти. Иногда это явление называют утечкой памяти .

15.4. Освобождение операцией delete памяти, которая не была выделена динамически операцией new.

15.5. Ссылка на область памяти, которая была освобождена.

15.6. Не осуществляется установка указателя связи на нуль в узле, являющемся дном стека.

15.7. Отсутствие установки указателя связи в последнем узле очереди в нуль (0).

15.8. Отсутствие установки указателей связи в нуль (0) в концевых узлах дерева.