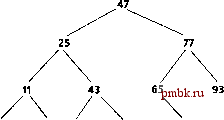7 17 31 44 68

Рис. 15.15. Дерево двоичного поиска

Программа, приведенная на рис. 15.16 (ее вывод представлен на рис. 15.17), создает дерево двоичного поиска и обходит его тремя способами: последовательным (симметричным) обходом (inorder), обходом в ширину (прямым обходом) (preorder) и обратным обходом (postorder). Программа генерирует 10 случайных чисел и помещает каждое из них в дерево, за исключением дублирующих значений, которые отбрасываются.

Давайте рассмотрим программу бинарного дерева, приведенную на рис. 15.16. Функция main начинает свою работу с создания экземпляра дерева двоичного поиска с данными целого типа intTree типа Tree<int>. Программа запрашивает 10 целых чисел, каждое из которых помещается в бинарное дерево путем обращения к insertNode. Затем программа выполняет последовательный (симметричный) обход, обход в ширину и обратный обход (эти варианты будут объяснены ниже) дерева intTree. После этого программа создает экземпляр дерева для данных с плавающей запятой floatTree типа Tree<float>. Программа запрашивает 10 данных с плавающей запятой, каждое из которых помещается в бинарное дерево путем обращения к insertNode. После этого программа выполняет последовательный (симметричный) обход, обход в ширину и обратный обход дерева floatTree.

Рассмотрим теперь описания шаблона класса и функций-элементов. Начнем с шаблона класса TreeNode, который объявляет в качестве дружественного шаблон класса Tree. Класс TreeNode имеет в качестве закрытых данных значения в узлах data и указатели leftPtr (указатель на узлы левого поддерева) и rightPtr (указатель на узлы правого поддерева). Конструктор задает в качестве начального значения data значение, которое он получает в качестве аргумента, и устанавливает указатели leftPtr и rightPtr в нуль (таким образом, узел инициализируется как концевой). Функция-элемент getData возвращает значение data.

Класс Tree имеет в качестве закрытых данных rootPtr - указатель на корневой узел дерева. У класса имеются открытые функции-элементы in-

В этом разделе создается особое бинарное дерево, которое называется деревом двоичного поиска (дихотомии). Дерево двоичного поиска (без дублирующих значений узлов) имеет характерную особенность, заключающуюся в том, что значение в любом узле левого поддерева меньше значения в его родительском узле, а значение в любом узле его правого поддерева больше значения в его родительском узле. На рис. 15.15 показано дерево двоичного поиска с 12-тью значениями. Заметим, что вид дерева двоичного поиска, соответствующий набору меняющихся данных, зависит от последовательности, в которой значения помещаются в дерево.

TREENODE.Н: Определение класса TreeNode

#ifndef TREENODE H #define TREENODE H

template<class NODETYPE> class TreeNode {

friend class Tree<NODETYPE>; public:

TreeNode(const NODETYPE &); конструктор

NODETYPE getDataO const; возвращение данных

private:

TreeNode *leftPtr; указатель на левое поддерево

NODETYPE data;

TreeNode *rightPtr; указатель на правое

поддерево

Конструктор template<class NODETYPE>

TreeNode<NODETYPE>::TreeNode(const NODETYPE &d) {

data = d;

leftPtr = rightPtr = 0;

Возвращение копии значений данных template<class NODETYPE>

NODETYPE TreeNode<NODETYPE>::getData() const { return data; } #endif

sertNode (которая помещает узел в дерево), preOrderTraversal, inOrderTrav-ersal и postOrderTraversal, каждая из которых обходит дерево заданным способом. Каждая из этих функций-элементов вызывает свою собственную отдельную рекурсивную функцию-утилиту для выполнения соответствующих операций над внутренней структурой дерева. Конструктор класса Tree задает указателю rootPtr нулевое значение, чтобы показать, что дерево в исходном состоянии является пустым.

Функция-утилита insertNodeHelper класса Tree рекурсивно помещает узел в дерево. Узел может быть помещен в дерево двоичного поиска только в качестве концевого узла. Если дерево является пустым, то создается новый экземпляр класса TreeNode, который инициализируется, и узел помещается в это дерево.

Если дерево не является пустым, то программа сравнивает вставляемое в дерево значение со значением data в корневом узле. Если вставляемое значение меньше значения в корневом узле, то программа рекурсивно вызывает утилиту insertNodeHelper для того, чтобы вставить значение в левое поддерево. Если вставляемое значение больше значения в корневом узле, то программа рекурсивно обращается к insertNode для того, чтобы поместить значение в правое поддерево. Если вставляемое значение равно значению данных в корневом узле, то программа печатает сообщение дубликат и возвращается, не вставив этот дубликат в дерево.

template<class NODETYPE> Tree<NODETYPE>::Tree0 { rootPtr =0; }

template<class NODETYPE>

void Tree<NODETYPE>::insertNode(const NODETYPE Evalue) { insertNodeHelper(SrootPtr, value); }

Эта функция принимает указатель на указатель, так что указатель может быть модифицирован. template<class NODETYPE>

void Tree<NODETYPE>::insertNodeHelper (TreeNode<NODETYPE> **ptr,

const NODETYPE Svalue)

if (*ptr == 0) { пустое дерево

*ptr = new TreeNode<NODETYPE>(value); assert(*ptr != 0);

else дерево не пустое

if (value < (*ptr)->data)

insertNodeHelper( &((*ptr)->leftPtr), value); else

if (value > (*ptr)->data)

insertNodeHelper (& ( (*ptr)->rightPtr), value); else

cout value дубль endl;

TREE.H: Определение шаблона класса Tree

#ifndef TREE H #define TREE H

tinclude <iostream.h> #include <assert.h> Iinclude treenode.h

template<class NODETYPE> class Tree { public: Tree();

void insertNode(const NODETYPE &); void preOrderTraversal() const; void inOrderTraversal() const; void postOrderTraversal () const; private:

TreeNode<NODETYPE> *rootPtr;

функции утилиты

void insertNodeHelper(TreeNode<NODETYPE> **, const NODETYPE &); void preOrderHelper(TreeNode<NODETYPE> *) const; void inOrderHelper(TreeNode<NODETYPE> *) const; void postOrderHelper(TreeNode<NODETYPE> *) const;