имен атрибутов (как и в рассмотренной выше операщш декартова произведения) и 0 определяется так же, как и в oпepaщи выборки. Тогда ©-соединением отношения А по атрибуту X с отношением В по атрибуту Y называется результат вычисления следующего выражения.

( А TIMES В ) WHERE X 0 У

Другими словами, 0-соединение - это отношение с тем же заголовком, что и при декартовом произведении отношений А и В, и с телом, содержащим множество кортежей t, таких, что кортеж t принадлежит этому декартову произведению и вычисление условия X 0 Y для кортежа t дает значение истина.

В качестве примера предположим, что необходимо вычислить больше чем -соединение отношения S по атрибуту CITY с отношением Р по атрибуту CITY (предполагается, что операция > имеет смысл для сравнения названий городов и интерпретируется просто как далее в алфавитном порядке ). Соответствующим выражением реляционной алгебры будет следующее.

( ( S RENAME CITY AS SCITY ) TIMES ( P RENAME CITY AS PCITY ) )

WHERE SCITY > PCITY

Обратите внимание на переименование атрибутов в этом примере. Конечно, достаточно было бы переименовать лишь один из двух атрибутов CITY. Единственный смысл двойного переименования - это симметрия. Результат вычисления данного выражения показан на рис. 6.7.

Puc. 6.7. Больше чем -соединение отношений поставщиков и деталей по атрибуту названия города

Если условие 0 является условием равно , то 0-соединение называется равно-соединением. Из определения следует, что результат равно-соединения должен включать два атрибута, значения которых должны быть равны в каждом кортеже отношения. Если исключить один из этих атрибутов (с помощью операции проекции), результатом будет обычное естественное соединение! Например, выражение, представляющее естественное соединение отношений поставщиков и деталей (по атрибуту города) S JOIN Р, эквивалентно следующему более сложному выражению.

( ( S TIMES ( Р RENAME CITY AS PCITY ) )

WHERE CITY = PCITY )

{ ALL BUT CITY }

Замечание. В языке Tutorial D нет прямой поддержки оператора 0-соединения, поскольку он не так уж часто используется на практике и, как мы уже видели, не является примитивным.

Деление

в [6.3] вводятся два разных оператора деления- Small Divide и Great Divide. В языке Tutorial D оператору <деление>, список <рег> которого состоит только из одного параметра <реляционное выражение>, соответствует операция Small Divide, а оператору <деление>, список <рег> которого состоит из двух разделенных запятыми параметров <реляционное выражение>, соответствует операция Great Divide. Приведенное далее описание относится только к частному ограниченному случаю операции Small Divide. Оператор Great Divide и подробности, касающиеся операции Small Divide, приводятся в [6.3].

Необходимо сказать, что рассмотренная здесь версия оператора Small Divide отличается от оригинального оператора, предложенного Коддом. Фактически это улучшенная версия, в которой исправлены недостатки, вызывавшие трудности при работе с пустыми отношениями. Данная версия также отличается от оператора Small Divide, рассмотренного в нескольких первых изданиях настоящей книги.

Дадим теперь определение оператора деления. Пусть отношения А и В имеют заголовки { XI, Х2, ... , Хт } и { Y1, Y2, ... , Yn } соответственно (т.е. заголовки отношений А и В не пересекаются). Пусть также отношение С имеет следующий заголовок.

{ XI, Х2, ... , Хт, Y1, Y2, ... , Yn } .

(Иначе говоря, заголовок отношения С является объединением заголовков отношений А и В.) Далее будем рассматривать множества { XI, Х2, ... , Хт } и { Y1, Y2, ... , Yn } как составные атрибуты X и Y соответственно. Тогда результатом деления отношения А на отношение В по отношению С (что записывается как А DIVIDEBY В PER С, где отношение А представляет собой делимое, отношение В - делитель, а отношение С- посредник ) называется отношение с заголовком {X} и телом, содержащим множество всех кортежей вида {Х:х}, таких, что кортеж вида {Х:х, Y:y} принадлежит отношению В для всех кортежей вида {Y:y}, принадлежащих отношению В. Нестрого это можно сформулировать так: результат содержит такие Х-значения из отношения А, для которых соответствующие Y-значения из отношения С включают все Y-значения из отношения В.

На рис. 6.8 показаны некоторые простые примеры операции деления. В каждом случае делимое (отношение DEND) - это проекция текущего значения переменной-отношения S по атрибуту S#, посредник (MED)- это проекция текущего значения переменной-отношения SP по атрибутам S# и Р#, а три делителя (отношения DOR)- такие, как показано на рисунке. В частности, обратите внимание на последний пример, в котором делителем является отношение, содержащее номера всех известных в данный момент деталей. В результате, очевидно, получим номера поставщиков, поставляющих все типы этих деталей. Как видно из примера, оператор DIVIDEBY полезен именно для запросов такого рода. Более того, если запрос на обычном языке включает слово все ( определить поставщиков всех типов деталей ), то почти наверняка понадобится использовать операцию деления. Тем не менее следует отметить, что подобные запросы удобнее записывать в терминах реляционных сравнений (раздел 6.9).

Действительно, операция деления задумывалась Коддом как алгебраический аналог квантора всеобщности (глава 7), а проекция - как алгебраический аналог квантора существования.

DEND

S# SI S2 S3 S4 S5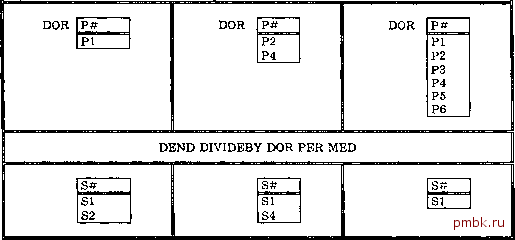

Puc. 6.8. Примеры операции деления

Ассоциативность и коммутативность

Легко проверить, что операция объединения (UNION) ассоциативна, т.е. если А, В и С - произвольные реляционные выражения (дающие совместимые по типу результаты), то приведенные ниже два выражения логически эквивалентны.

( А UNION В ) UNION С А UNION ( В UNION С )

Следовательно, для удобства можно разрешить запись последовательных операторов объединения без использования круглых скобок. Поэтому предыдущие выражения можно однозначно упростить следующим образом.

А UNION В UNION С

Аналогичные замечания можно сделать и для операций пересечения (INTERSECT), декартова произведения (TIMES) и соединения (JOIN) (но не операции вычитания MINUS).

Заметим также, что операции объединения (UNION), пересечения (INTERSECT), декартова произведения (TIMES) и соединения (JOIN) (но не операция вычитания MINUS) еще и коммутативны, т.е. выражения А UNION В и В UNION А эквивалентны, что справедливо и для операций пересечения, декартова произведения и соединения.