точно экзотический). Смысл каждого кортежа {S:s, J: j, T:t} переменной-отношения SJT состоит в том, что некоторый студент s изучает некоторый предмет j у некоторого преподавателя t. При этом на информацию накладываются следующие два офаничения.

Каждый студент изучает определенный предмет только у одного преподавателя.

Каждый преподаватель ведет только один предмет, однако каждый предмет может преподаваться несколькими преподавателями.

На рис. 11.14 показан пример данных в переменной-отношении SJT.

Puc. 11.14. Пример данных в переменной-отношении SJT

Какие функциональные зависимости сушествуют в этой переменной-отношении? Из первого Офаничения следует зависимость атрибута Т от комбинации атрибутов {S, J}, а из второго - зависимость атрибута J от атрибута Т. Следовательно, диафамма функциональных зависимостей переменной-отношении SJT будет иметь вид, представленный на рис. 11.15.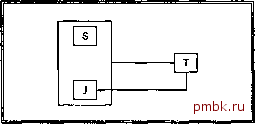

Рис. 11.15. Диаграм-ма функциональных зависимостей в переменной-отношении SJT

И вновь в рассматриваемом примере присутствуют два перекрывающихся потенциальных ключа, а именно: комбинация {S, J} и комбинация {S, Т}. Как и в первом примере, исходная переменная-отношение SJT находится в ЗНФ, но не в НФБК, в связи с чем для нее будут характерны некоторые аномалии обновления. Например, если потребуется удалить сведения о том, что студент Джонс (Jones) изучает физику, этого нельзя будет сделать, не утратив одновременно информацию о том, что профессор Браун (Prof. Brown) преподает этот предмет. Подобные трудности вызваны тем, что атрибут Т является детерминантом, но не является потенциальным ключом. И вновь для решения указанной проблемы исходную переменную-отношение SJT следует разбить на две проекции, каждая из которых будет находиться в НФБК.

ST { S, Т } TJ { Т, J }

в качестве упражнения читателю предлагается составить таблицы с данными этих двух переменных-отношений (исходя из набора данных, представленных на рис. 11.14), а также нарисовать соответствующую диафамму ФЗ для проверки, действительно ли две созданные проекции находятся в НФБК (какие атрибуты являются их потенциальными ключами?). Кроме того, читателю рекомендуется проверить тот факт, что данная декомпозиция позволяет устранить все существовавшие ранее аномалии обновления.

Однако следует отметить, что все еще существует иная проблема. Суть ее в том, что декомпозиция исходного отношения на проекции ST и TJ позволила исключить одни аномалии, однако привела к появлению других. Причиной является тот факт, что проекции ST и TJ не являются независимыми в смысле Риссанена (подробности приводятся выше в данной главе). Точнее говоря, функциональная зависимость {S, J} -> Т не может быть выведена из той единственной функциональной зависимости, которая присутствует в двух данных проекциях (Т J).

В результате две полученные проекции не могут обновляться независимо. Например, попытка вставить в переменную-отношение ST кортеж для студента Смита (Smith) и профессора Брауна (Prof. Brown) должна быть отвергнута системой, поскольку профессор Браун преподает физику, а Смит уже обучается физике у профессора Грина (Prof. Green). Однако обнаружить этот факт, не проверив содержимое переменной-отношения TJ, система не может. Таким образом, мы пришли к неприятному выводу о том, что попытка достижения двух целей, а именно - декомпозиции исходной переменной-отношения на переменные-отношения, находящиеся в НФБК, и декомпозиции исходной переменной-отношения на независимые компоненты, в некоторых случаях может привести к конфликтной ситуации. Поэтому достичь обе цели одновременно не всегда возможно.

Замечание. В действительности переменная-отношение SJT является атомарной (см. раздел 11.4) даже несмотря на то, что она не находится в НФБК. Однако тот факт, что атомарная переменная-отношение не может быть подвергнута декомпозиции на независимые компоненты, отнюдь не означает, что она вообще не может быть подвергнута декомпозиции (здесь под декомпозицией понимается декомпозиция без потерь). Атомарная переменная-отношение - не совсем подходящий термин для данной концепции, по крайней мере с интуитивной точки зрения, поскольку подобная атомарность не является ни необходимым, ни достаточным условием создания хорошего проекта базы данных.

В качестве третьего и последнего примера переменной-отношения с перекрывающимися потенциальными ключами рассмотрим переменную-отношение EXAM с атрибутами S (студент), J (предмет) и Р (позиция). Каждый кортеж {S:s, J:j, Р:р} переменной-отношения EXAM отражает сведения о том, что некоторый студент s экзаменуется по определенному предмету j и занимает определенную позицию р в списке экзаменующихся. Дополнительно условимся, что в нашем примере имеет место следующее ограничение.

Никакие два студента не могут занимать одну и ту же позицию в списке экзаменующихся по одному и тому же предмету.

В этом случае диаграмма функциональных зависимостей будет иметь вид, представленный на рис. 11.16.

Рис. 11.16. Диаграмма функциональных зависимостей в переменной-отношении EXAM

В этом примере вновь присутствуют два перекрывающихся потенциальных ключа, {S, J}h{J, Р}, поскольку для каждого студента и предмета существует точно одна занимаемая позиция в соответствующем списке, а в каждом списке экзаменующихся по некоторому предмету каждую позицию занимает только один соответствующий студент. Однако такая переменная-отношение находится в НФБК, поскольку указанные потенциальные ключи являются ее единственными детерминантами. Поэтому для данной переменной-отношения не характерны какие-либо аномалии обновления, подобные упоминавшимся ранее в настоящей главе. (Упражнение. Проверьте правильность этого утверждения.) Таким образом, наличие перекрывающихся потенциальных ключей не всегда приводит к появлению проблем подобного рода.

В заключение следует подчеркнуть, что концепция НФБК позволяет избавиться от проблем, которые присущи формам, соответствующим старому определению ЗНФ. Более того, новое определение концептуально проще старого, так как в нем не используются понятия 1 НФ, 2НФ, первичного ключа или транзитивной зависимости. Дополнительно понятие потенциального ключа может быть заменено ссылкой на более фундаментальное понятие функциональной зависимости (в определении, данном в [11.2], имеет место именно такая замена). С другой стороны, концепции первичного ключа, транзитивной зависимости и т.д. весьма полезны на практике, поскольку позволяют сформулировать идею некоторого пошагового процесса, выполняемого разработчиком для приведения произвольной переменной-отношения к эквивалентному набору переменных-отношений в НФБК.

Наконец заметим, что в ответе к упр. 11.3 приведен алгоритм, по которому произвольная переменная-отношение может быть подвергнута декомпозиции без потерь информации с ее преобразованием в набор проекций, находящихся в НФБК.

11.6. Замечание по поводу атрибутов, содержащих в качестве значений отношения

Как было показано в главе 5, отношение может содержать атрибут, значения которого также являются некоторыми отношениями (рис. 11.17). Конечно, следствием этого является тот факт, что переменная-отношение, в свою очередь, также может содержать атрибуты, значениями которых являются некоторые переменные-отношения. Однако с точки зрения процедуры проектирования базы данных использовать подобные перемен-