обратном соединении переменных-отношений SST и SC исходная переменная-отношение S получена не будет, а это значит, что некоторая информация будет утрачена. Иначе говоря, обратимость означает, что исходная переменная-отношение равна соединению ее проекций. Если оператором декомпозиции в процедуре нормализации является операция проекции, то обратной операцией должна быть операция соединения.

Исходя из сказанного выше, можно задать следующий вопрос. Пусть R1 и R2 являются проекциями некоторой переменной-отношения R, содержащими все атрибуты переменной-отношения R. Какие условия должны быть соблюдены для того, чтобы при обратном соединении проекций R1 и R2 гарантировать получение исходной переменной-отношения R? IMCHHo для получения ответа на этот вопрос необходимо обратиться к функциональным зависимостям. В рассматриваемом примере переменная-отношение S удовлетворяет представленному неприводимому множеству функциональных зависимостей.

St STATUS Si CITY

При условии, что данная переменная-отношение удовлетворяет приведенным функциональным зависимостям, можно предположить, что переменная-отношение S равна соединению ее проекций {SI, STATUS} и {Si, CITY}. И это действительно так, что подтверждается теоремой Хита (Heath) [11.4].

Теорема Хита. Пусть R{A, В, С} является переменной-отношением, где А, В и С - множества атрибутов этой переменной-отношения. Если R удовлетворяет функциональной зависимости А В, то R равна соединению ее проекций {А, В} и{А, С}.

Если принять, что А- это атрибут Si, В- это атрибут STATUS, а С- это атрибут CITY, то данная теорема подтверждает, как отмечалось выше, что переменная-отношение S может быть разбита с помощью операции декомпозиции на проекции {Si, STATUS} и {Si, CITY} без потери информации.

В то же время уже известно, что переменная-отношение S не может быть разбита без потери информации на проекции {Si, STATUS} и {STATUS, CITY}. Теорема Хита не дает объяснения, почему так происходит. Однако интуитивно можно предположить, что при такой декомпозиции утрачивается одна из функционачьных зависимостей, т.е. зависимость Si -н STATUS будет присутствовать (благодаря проекции {Si, STATUS}), а зависимость Si CITY будет утрачена.

Точнее, в исходной переменной-отношении S вместе со всеми кортежами будут содержаться ложные кортежи, поскольку при обратной операции никогда нельзя получить переменную-отношение, которая была бы меньше исходной переменной-отношения S (Упражнение Попробуйте доказать это утверждение) Поскольку не существует общего метода различения ложных и подлинных кортежей, информация в этом случае действительно будет утеряна

Дело в том, что она формулируется в выражениях если , то , а не тогда и только тогда, когда Об этом также идет речь в упр 111 Более строгая формулировка теоремы Хита будет представлена в следующей главе (в разделе 12 2)

Еще о функциональных зависимостях

в завершение перечислим некоторые дополнительные замечания, касающиеся функциональных зависимостей.

1. Неприводимые слева ФЗ. Вспомним из главы 10, что функциональная зависимость называется неприводимой слева, если ее левая часть не очень велика . Рассмотрим, например, переменную-отношение SCP, приведенную в разделе 11.1, которая удовлетворяет следующей функциональной зависимости.

{ Si, Pi } CITY

Однако атрибут Pi в левой части этой функциональной зависимости является избыточным и она может быть переписана в следующем виде.

Si -> CITY

(Иначе говоря, атрибут CITY функционально зависит от St.) Эта последняя функциональная зависимость является неприводимой слева, а предыдущая - нет. Таким образом, можно сказать, что атрибут CITY неприводимо зависим от атрибута Si, но не неприводимо зависим от множества атрибутов {Si, Pi}.

Неприводимые слева ФЗ и неприводимые зависимости ифают важную роль при определении второй и третьей нормальной форм (подробности приводятся в разделе 11.3).

2. Диаграммы ФЗ. Пусть дана переменная-отношение R и пусть к ней применимо некоторое неприводимое множество функциональных зависимостей I (более подробные сведения о неприводимых множествах ФЗ приводятся в главе 10). Удобнее всего представить это множество ФД в виде диаграммы функциональных зависимостей (диаграммы ФЗ). Например, на рис. 11.4 показаны вполне очевидные по смыслу диаграммы функциональных зависимостей для переменных-отношений S, SP и Р соответственно. Такие диаграммы будут часто использоваться далее в этой главе.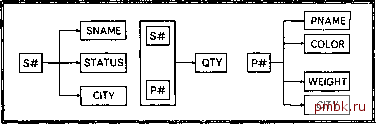

Рис. 11.4. Диаграм.ма функционапьных зависимостей для переменных-отношений S, SPu Р

Как можно видеть, на рис. 11.4 каждая стрелка начинается с потенциального ключа (на самом деле- с первичного ключа) соответствующей переменной-отношения. По определению стрелки должны начинаться с каждого потенциально-

Здесь термины неприводимая слева ФЗ и неприводимо зависим используются вместо терминов полная ФЗ и полностью зависим , которые часто можно встретить в литературе и прежнга изданиях этой книги. Хотя последние термины отличаются краткостью, они менее информативны и потому не очень удобны.

го ключа, поскольку одному значению такого ключа всегда соответствует еще по крайней мере одно какое-либо значение. Некоторые из существующих стрелок в определенных случаях необходимо будет искчючить ввиду того, что они вызывают определенные затруднения, однако стрелки, начинающиеся с потенциальных ключей, никогда не могут быть исключены. Таким образом, процедуру нормализации можно неформально охарактеризовать как процедуру исключения стрелок, которые не начинаются с потенциальных ключей. 3. ФЗ как семантическое понятие. Конечно, функциональные зависимости- это особый вид ограничений целостности, а потому они, несомненно, являются понятием семантическим. Распознавание функциональных зависимостей представляет собой часть процесса выяснения смысла тех или иных данных. Тот факт, что переменная-отношение S удовлетворяет зависимости Si CITY, по сути, означает, что каждый поставщик находится точно в одном городе. Иначе эту ситуацию можно охарактеризовать следующим образом.

В реальном мире существует некоторое ограничение, представленное в этой базе данных, а именно: каждый поставщик находится точно в одном городе.

Поскольку это ограничение является частью семантического описания предметной области, оно должно быть каким-то образом представлено в базе данных.

Для этого Офаничение необходимо описать в определении базы данных таким образом, чтобы оно могло быть приведено в действие средствами СУБД.

Способ описания ограничения в определении базы данных состоит в объявлении соответствующей функциональной зависимости.

Как будет показано ниже, концепции нормализации позволяют использовать весьма простые способы объявления ФЗ.

11.3. Первая, вторая и третья нормальные формы

Предостережение. В этом разделе для простоты изложения предполагается, что каждая переменная-отношение имеет в точности один потенциальный ключ, который является первичным ключом. Подобное допущение нашло отражение в приведенных ниже доказательствах, которые (как уже от.мечалось) являются не очень строгими. Далее, в разделе 11.5, будет рассмотрен случай, когда переменная-отношение имеет два или более потенциальных ключей.

Прежде чем перейти к подробному описанию трех нормальных форм, исходно предложенных Коддом, следует дать предварительное и весьма неформальное определение третьей нормальной формы для того, чтобы в общих чертах обрисовать основную цель изложения. Затем будет рассмотрена процедура приведения произвольной переменной-отношения к эквивалентному набору переменных-отношений в ЗНФ. Попутно будут даны более точные определения первых трех нормальных форм. Однако в качестве отступления следует отметить, что формы 1НФ, 2НФ и ЗНФ сами по себе не имеют особого значения и должны рассматриваться лишь как промежуточные этапы на пути построения формы НФБК (и форм более высокого уровня).

Точнее, стрелки должны начинаться с суперключей. Но если множество ФЗ является неприводимым, все функциональные зависимости (или стрелки ) будут неприводимы слева.