Я называют эти нефильтрованные внешние соединения вниз с простыми таблицами нормальными внешними соединениями. У нормальных внешних соединений есть особое полезное с точки зрения оптимизации свойство: количество строк, оставшееся после вьшолнения нормального внешнего соединения, равно количеству строк перед выполнением этого соединения.

Это свойство делает рассмотрение нормального внешнего соединения особенно простым - нормальные внешние соединения никак не влияют на текущее количество строк (количество строк, считанное в любой точке порядка соединения). Таким образом, они несущественны для оптимизации оставшейся части запроса. Главная причина, почему следует выполнять соединения вниз перед соединениями вверх, уже не играет роли. Нормальные внешние соединения, в отличие от внутренних соединений, не могут сократить количество строк, которое передается в дальнейшие, более дорогие соединения вверх. Так как они не влияют на оставшуюся часть задачи оптимизации, то вам следует просто выбрать точку в порядке соединения, где стоимость нормального внешнего соединения сама по себе минимальна. Это точка, в которой текущее количество строк минимально, но после того, как присоединяемая внешне таблица становится доступна в дереве соединения.

Шаги порядка оптимизации нормального внешнего соединения

Свойства нормальных внешних соединений приводят нас к новому набору шагов, подходящих для оптимизации запросов с такими соединениями.

1. Изолируйте часть диаграммы соединения, в которой нет нормальных внешних соединений. Назовем ее внутренней диаграммой запроса.

2. Оптимизируйте внутреннюю диаграмму запроса, не учитывая нормальные внешние соединения.

3. Разделите узлы, присоединяемые внешне в нормальных внешних соединениях, на поднаборы согласно тому, на каком уровне они прикреплены к внутренней диаграмме запроса. Назовем поднабор, прикрепленный к ведущей таблице или под ней, s 0. Набор, к которому можно перейти только через одно соединение вверх от ведущей таблицы, - s l. Набор, к которому можно перейти только через два соединения вверх от ведущей таблицы, - s 2, и так далее.

4. Подсчитайте относительное текущее количество строк для каждой точки в порядке соединения перед следующим соединением вверх и для конечной точки порядка соединения.

ПРИМЕЧАНИЕ

Под относительным текущим количеством строк я подразумеваю, что вы можете выбрать любое начальное значение количества строк, просто для удобства подсчетов, если после этой точки все вычисления будут непротиворечивы.

Назовем относительное текущее количество строк перед первым соединением вверх г 0; относительное текущее количество строк перед вторым соединени-

ем вверх г 1; и так далее. Назовем конечное относительное количество строк ! }, где j - количество соединений вверх от ведущей таблицы к корневой детальной таблице.

5. Среди всех поднаборов s n найдите минимальное значение r m (так, чтобы m > п) и присоедините все узлы в этом поднаборе сверху вниз в точке порядка соединения, где относительное количество строк равно этому минимальному значению. Присоедините последний поднабор, прикрепленный внизу к корневой детальной таблице, в конце порядка соединения после всех внутренних соединений, так как это единственный допустимый минимум для этого поднабора.

Пример

Эти шаги требуют более глубокого рассмотрения. Чтобы применить шаги 1 и 2 к рис. 9.1, рассмотрим рис. 9.2.

М0.5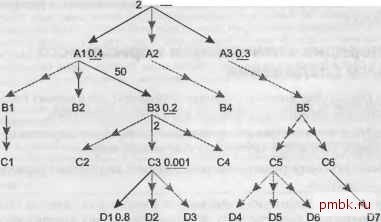

Рис. 9.2. Внутренняя диаграмма запроса для предыдущего запроса

Первоначальное сложное 22-стороннее соединение мы сократили до 6-сторон-него соединения, показанного на внутренней диаграмме запроса черным цветом. Это простая задача оптимизации, для которой легко находится лучший порядок внутренних соединений (СЗ. D1, ВЗ. А1. М. A3).

Теперь перейдем к шагу 3. Ведущая таблица - это СЗ, поэтому поднабор s 0 содержит все нормальные присоединяемые внешне таблицы, доступные через соединения вниз от СЗ. Это набор {D2. 03}. Первое соединение вверх - это соединение с ВЗ, поэтому s l состоит из {С2, С4} - набора узлов (исключая узлы из поднабора s 0), достижимых через соединения вниз от ВЗ. Второе соединение вверх проводится с А1, поэтому s 2 выглядит как {В1, В2, С1}. Последнее соединение вверх - это соединение с М, поэтому в s 3 содержатся все остальные нормальные присоединяемые внешне таблицы: {А2. В4. В5. С5. Сб. D4. D5, D6. D7}. На рис. 9.3 показано, как присоединяемые внешне таблицы разделены на поднаборы.

Теперь перейдем к шагу 4. Так как нам нужны только сравнительные (или относительные) текущие количества строк, пусть начальное количество строк в СЗ будет любым числом, на основе которого можно будет выбрать удобное круглое значение г 0, например, 10. Начиная с этого значения, найдем список значений для г п.

г 0:10 - выбрано произвольно, лишь для упрощения подсчетов.

г 1: 6 (г 0 x 3 x 0,2) - числа 3 и 0,2 - это детальный коэффициент соединения для соединения с ВЗ и произведение всех коэффициентов фильтрации, собранных до следующего соединения вверх. Также нужно было бы скорректировать количества строк в зависимости от главных коэффициентов соединения, меньших 1,0, если бы такие существовали, но в нашем примере только обычные главные коэффициенты соединения, равные 1,0. Так как под ВЗ нет фильтрованных узлов, которые обрабатываются после соединения с ВЗ, единственный значимый фильтр - это фильтр для ВЗ, коэффициент фильтрации которого равен 0,2.

2 М 05

Рис. 9.3. Поднаборы присоединяемых внешне таблиц для предыдущего запроса

г 2: 120 (г 1 x 50 x 0,4) - числа 50 и 0,4 это детальный коэффициент соединения для соединения с А1 и произведение всех коэффициентов фильтрации, собранных до следующего соединения вверх. Так как ниже А1 нет фильтрованных узлов, которые обрабатываются после соединения с А1, единственный значимый фильтр - это фильтр для А1, коэффициент фильтрации которого равен 0,4.

г 3:36 (г 2 x 2 x 0,15) - числа 2 и 0,15 являются детальными коэффициентами соединения для связи с М и произведением всех оставшихся коэффициентов фильтрации. Так как после соединения с М обрабатывается один фильтрованный узел A3, то произведением всех оставшихся коэффициентов фильтрации является произведение коэффициента фильтрации для М (0,5) и коэффициента фильтрации для A3 (0,3): 0,5x0,3 = 0,15.