рядок соединения будет таким же, какой вы бы выбрали, если бы не знали, что условие фильтрации уникально. Однако когда наилучший фильтр не уникальный, лучший порядок соединения может прыгать по скелету соединения, то есть вторая таблица может считываться не через ключ соединения, указывающий на первую таблицу.

Детальные коэффициенты фильтрации, близкие к 1,0

Рассматривайте соединения вверх как соединения вниз, когда коэффициент фильтрации близок к 1,0 и когда это позволяет получить доступ к полезным фильтрам (с меньшими коэффициентами фильтрации) как можно раньше в плане выполнения. Если сомневаетесь в разумности подобного подхода, попробуйте оба варианта. На рис. 6.18 показан случай, когда два из существующих соединений вверх не хуже, чем существующие соединения вниз. Перед тем, как прочитать решение, попробуйте решить задачу самостоятельно.

Как обычно, начните с наилучшего фильтра, соответствующего В4, и используйте индекс. Затем переходите к остальным таблицам через вложенные циклы по индексам по ключам соединения. В отличие от предьщущих случаев, до того как рассмотреть соединения вверх с коэффициентами соединения, равными 1,0, не нужно выполнять все соединения вниз.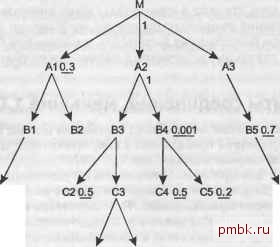

С10.6

С6 0.9

DIOJ D2

Рис. 6.18. Случай с детальными коэффициентами соединения, равными 1,0

ПРИМЕЧАНИЕ

Очевидно, здесь есть соединения вида один ко многом , очень близкие к один к одному Также существуют соединения один к нулю и один ко многим , где случаи один к нулю аннулируют увеличение количества строк после выполнения соединений один ко многим . В любом случае, с точки зрения оптимизации, это практически то же самое, что соединения один к одному .

Как обычно, найдите фильтры в соседних узлах. Две первые лучшие возможности - это С5, а затем С4. Затем у вас есть только одна возможность - выполнить соединение вверх к нефильтрованному узлу А2, которое вы бы выполнили следующим, даже если детальный коэффициента соединения был бы велик. Получается, что небольшой коэффициент соединения с А2 не играет роли. На данный момент порядок соединения (В4. С5. С4. А2).

Из облака вокруг этих узлов найдите соседние узлы ВЗ (вниз) и М (вверх). Так как детальный коэффициент соединения с М равен 1,0, то, если прочие фа1сгоры говорят в пользу М, не нужно выбирать соединение вниз. Ни у одного из узлов нет фильтра, поэтому посмотрите на фильтры для узлов, соседних с рассматриваемыми узлами. Лучший коэффициент фильтрации рядом с М равен 0,3 (для А1), а лучший коэффициент фильтрации рядом с ВЗ равен 0,5 (для С2), поэтому мы выбираем присоединение М, а затем А1. Сейчас порядок соединения (В4. С5. С4. А2. М. А1). Теперь, когда база данных пришла к корневому узлу, все соединения будут вести вниз, поэтому можно применять обычные правила оптимизации, выбирая из примыкающих к облаку узлов и для решения спорных вопросов рассматривая узлы, соседние с данными. Полный оптимальный порядок соединения (В4. С5. С4. А2. М. А1, ВЗ. С2. В1. С1. A3. В5. Сб. СЗ. D1. (D2. В2)).

ПРИМЕЧАНИЕ-

Запись (D2, В2) в конце порядка соединения указывает, что порядок двух последних узлов не играет роли.

Обратите внимание, что даже в этом особом случае, предназначенном для демонстрации исключения из предыдущих правил, мы получаем лишь небольшое улучшение благодаря более раннему доступу к А1, чем позволила бы простая эвристика, так как это улучшение встречается в порядке соединения достаточно поздно.

Коэффициенты соединения, меньшие 1,0

Если детальный или главный коэффициент соединения меньше 1,0, то это соединение фактически в среднем принадлежит к виду [некоторое число] к [меньше, чем 1,0] . Может ли сторона меньше, чем 1,0 этого соединения принадлежать виду ко многим - для проблемы оптимизации несущественно, если вы уверены, что текущее среднее количество связанных данных не должно сильно измениться для других экземпляров баз данных. Если соединение вниз с обычным главным коэффициентом соединения, равным 1,0, предпочтительней, чем соединение вверх вида ко многим , то соединение в любом направлении с коэффициентом, меньшим 1,0, является более предпочтительным. Эти коэффициенты соединения, меньшие 1,0, в каком-то смысле являются скрытыми фильтрами, которые при выполнении соединения отбрасывают строки так же эффеетивно, как и явные одно-узловые фильтры, и поэтому влияют на оптимальный порядок соединения так же, как фильтры.

Правила для коэффициентов соединения, меньших 1,0

Чтобы учесть эффект небольших коэффициентов соединения при выборе оптимального порядка соединения, вам потребуются три правила.

При выборе ведущего узла все узлы на фильтрованной стороне соединения наследуют дополнительные преимущества скрытого фильтра соединения. Например, если меньший 1,0 коэффициент соединения - это J, а коэффициент фильтрации узла равен R, при выборе наилучшего узла берите значение J ? R. При сравнении узлов на одной стороне фильтра соединения это не будет иметь никакого эффекта, но у узлов на фильтрованной стороне соединения будет преимущество перед узлами на стороне, не имеющей фильтра.

Выбирая следующий узел в последовательности, считайте все соединения с коэффициентом соединения J (меньшим 1,0) соединениями вниз. При сравнении узлов используйте эффисгивный коэффициент фильтрации J х R, где R - это коэффициент фильтрации одного узла, обращение к которому идет через это фильтрующее соединение.

Однако для главных коэффициентов соединения, меньших 1,0, рассмотрите, не будет ли лучше сделать скрытый фильтр явным фильтром вида внешний 1СПЮЧ не равен null . Превращение не null фильтра в явный позволяет детальной таблице, находящейся прямо над фильтрующим главным соединением, также наследовать селективность J х R во время выбора ведущей таблицы и порядка соединения сверху. Подробнее об этом правиле - в следующих разделах.

Детальные коэффициенты соединения, меньшие 1,0

Значение небольших коэффициентов соединения оказывается различным в зависимости от того, является ли коэффициент главным или детальным, меньшим 1,0. Детальный коэффициент соединения, меньший 1,0, означает, что когда отсутствие деталей определенного типа вообще более вероятно, чем наличие нескольких, вероятность появления нескольких деталей все же существует. Например, у вас может быть таблица Employees, связанная с таблицей Loans для отслеживания займов, которые компания делает нескольким менеджерам верхнего звена в качестве вознаграждения. Дизайн базы данных должен разрешать нескольким сотрудникам иметь несколько займов, но у гораздо большего количества сотрудников вообще не будет займов от компании, поэтому детальный коэффициент соединения будет близок к 0. Для обеспечения ссылочной целостности столбец Empl oyee ID таблицы Loans должен указывать на реального сотрудника. Это его единственное предназначение, и все займы в этой таблице будут относиться только к сотрудникам. Однако нет никакой необходимости, чтобы Empl oyee ID соответствовал какому-либо займу. Столбец Employee ID таблицы Employees существует (как и любой первичный ключ) только для того, чтобы указывать на собственную строку, а не на строки в другой таблице, поэтому не удивительно, что соединение не может найти соответствия по направлению вверх, от первичного ключа ко внешнему.

Так как обработка детальных коэффициентов соединения, меньших 1,0, оказывается делом простым, хотя и редко встречающимся, я проиллюстрирую этот случай. Проработаем пример из предыдущего абзаца, чтобы попытаться сделать новые правила более убедительными. Начнем с запроса, который присоединяет Empl oyees к Loans, и добавим соединение с Departments с фильтром, который отбрасывает по-