плохо работают на быстро растущих таблицах. Даже если размеры таблиц не увеличиваются, планы с декартовым произведением ведут себя менее предсказуемо, чем обычные планы, посколы<у коэффициенты фильтрации обычно представляют собой среднее значение среди всех возможных значений. Фильтр, пропускающий в среднем лишь одну строку, может иногда пропустить 5 или 10 строк, в зависимости от значений параметра. Если селективность фильтра для стандартного надежного плана меньше среднего, стоимость возрастает пропорционально количеству строк, которое вернет запрос. Если план с декартовым произведением применять с такими же непостоянными фильтрами, его стоимость может возрасти как квадрат изменения объема отфильтрованных данных или даже хуже.

Но иногда можно использовать декартовы произведения без опасений за ухудшение производительности, получая неожиданные преимущества. Вполне безопасно можно создавать декартовы произведения любого количества наборов, возвращающих гарантированно одну строку, получая недорогой, однострочный результат. Можно даже комбинировать однострочный набор с многострочным, и результат будет не хуже, чем если бы вы считали этот многострочный набор из ведущей таблицы отдельно. Основное преимущество надежных планов - тщательное исключение планов вьшолнения, которые сочетают несколько многострочных наборов. Вспомните, что в главе 5 правила требовали поместить звездочку рядом с уникальными условиями фильтрации (условиями, гарантированно пропускающими максимум одну строку). С тех пор я не использовал эти звездочки, но сейчас они снова выходят на сцену.

Рассмотрим рис. 6.15. Обратите внимание, что на нем есть два уникальных фильтра, для В2 и СЗ. Начиная с единственной строки из СЗ, которой соответствует уникальное условие фильтрации, вы можете быть уверены, что из D1 и D2 будет присоединено по одной строке через их первичные ключи (см. указывающие вниз стрелки к D1 и D2). Изолируйте эту ветвь, считая ее отдельным однострочным запросом. Теперь получите единственную строку из В2, которая удовлетворяет уникальному условию фильтрации, и объедините два независимых запроса декартовым произведением, чтобы получить комбинированный набор из одной строки.

Поместив эти однострочные запросы на первое место, вы получите начальный порядок соединения (СЗ. D1. D2. В2) (или (В2. СЗ. D1. D2), без разницы). Если вы будете считать первые запросы, выдающие однострочный результат, независимой операцией, то обнаружите, что для таблиц А1 и ВЗ получатся новые условия фильтрации, так как до того, как выполнить оставшуюся часть запроса, вы уже будете знать значения внешних ключей, указывающих на В2 и СЗ. Измененный запрос теперь выглядит как на рис. 6.16, на котором уже выполненные однострочные запросы помещены в серое облако, обозначающее границы уже считанного фрагмента запроса.

Указывающие вверх стрелки обозначают, что начальное условие фильтрации для А1 комбинируется с новым условием фильтрации по внешнему ключу, указывающему на В2, что дает общую селективность 0,06. Не фильтрованный ранее узел ВЗ получает из условия по внешнему ключу, указывающему на СЗ, коэффициент фильтрации 0,01.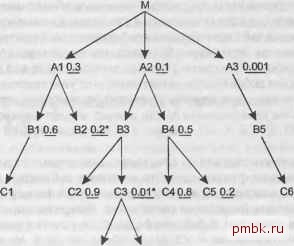

D1 D2

Рис. 6.15. Запрос с уникальными условиями фильтрации М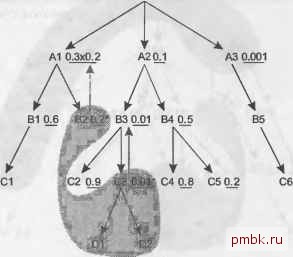

Рис. 6.16. Запрос с уникальными условиями фильтрации, с заранее считанными ветвями

однострочных операций

ВНИМАНИЕ

Обычно можно предположить, что любая данная часть строк главной таблицы будет соединяться с практически такой же по размерам частью строк детальной таблицы. Для таблиц транзакций, таких, как Orders и Order Detalls, это хорошее предположение. Однако небольшие таблицы часто предназначены для хранения типов или состояний, а в таблицах транзакций тины и состояния распределены неравномерно. Например, с 5-строчной таблицей состояний (которой может быть В2) какое-то состояние может соответствовать большинству строк транзакций или же всего нескольким. В подобных случаях, когда главная таблица содержит асимметричные значения, необходимо исследовать фактическое асимметричное распределение.

Теперь оставшуюся часть запроса за пределами облака можно оптимизировать как отдельную, следуя стандартным правилам. Оказывается, что A3 - это наилучшая ведущая таблица с лучшим коэффициентом фильтрации. (Неважно, что A3 не соединяется напрямую с В2 или СЗ, так как декартово произведение с однострочным набором безопасно.) Отсюда переходим к 85 и Сб, затем наверх к М. Так как А1 получила добавленную селективность от унаследованного фильтра по внешнему ключу, указывающему на В2, ее коэффициент фильтрации лучше, чем у А2, поэтому далее присоединяем А1. На данный момент порядок соединения - (СЗ. D1, D2. 82. A3. 85. Сб, М, А1), а запрос с облаком соединения выглядит как на рис. 6.17.

Так как мы заранее считали В2, следующие допустимые узлы - 81 и А2, и у А2 лучший коэффициент фильтрации. Это позволяет добавить в список допустимых узлы ВЗ и В4, и оказывается, что унаследованный фильтр для ВЗ делает его лучшим выбором для очередного соединения. Завершая порядок соединения, следуя обычным правилам, добавляем В4, С5, В1, С4, С2 и С1 в указанном порядке. Полный порядок соединения - (СЗ. D1. D2. 82. A3. 85. Сб. М. А1. А2. ВЗ. В4. С5, 81. С4. С2. С1).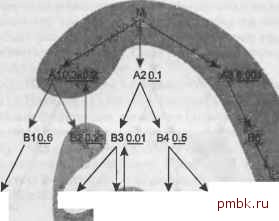

С20.9 CSmr. С4 0.8 С5 0.2

Рис. 6.17. Запрос с уникальными условиями фильтрации, с заранее полученными ветвями однострочных операций и облаком соединения вокруг считанных следующими пяти узлов

Даже если у вас есть только одно уникальное условие фильтрования, выполните этот процесс предварительного считывания одной строки из узла или ветви, передавая коэффициент фильтрации наверх к детальной таблице и оптимизируя оставшуюся часть диаграммы так, как если бы она существовала отдельно. Когда уникальное условие относится к какой-либо таблице транзакций, а не к таблице, хранящей типы или состояния, оно обычно характеризуется наилучшим коэффициентом фильтрации в запросе. В этом случае результирующий по-