настолько, насколько это необходимо и достаточно. Любое существенное упрощение этих правил приведет к пропуску больших и распространенных классов плохо настроенных запросов, а усложнение позволит добиться заметного улучшения только для относительно редких классов запросов.

ПРИМЕЧАНИЕ

Позже в этой книге я рассмотрю эти редкие случаи и объясню, что с ними делать, но сначала надо как можно глубже уяснить базовые принципы.

Нужно знать одну тонкость, которая появляется, когда в шагах 2 и 3 упоминаются очередные связи вверх или вниз, обозначающие соединения. Таблицы, уже обработанные в плане, объединяются в один виртуальный узел, чтобы упростить выбор следующего шага плана. Наверное, будет проще отображать уже обработанные таблицы как объединение узлов в виде облака. Для оставшейся части плана совершенно неважно, как организованы уже обработанные таблицы или в каком порядке к ним обращались. Ответ на вопрос Какая таблица идет следующей? совершенно не зависит от порядка или метода, которые вы использовали при соединении предыдущих таблиц. Таблицы, находящиеся в объединении, определяют его границы и важны для плана, но как они туда попали - это, грубо говоря, уже история, которая не относится к очередному решению.

Когда вы составляете план вьшолнения, то можете обнаружить, что выбрали ведущей только что присоединенную таблицу. Это, конечно, ошибка. Если таблицы присоединяются к любому члену набора уже соединенных таблиц, то они совершенно одинаково могут присоединяться снизу или сверху облака. По мере прохождения шагов процесса можно даже рисовать расширяющиеся таблицы облака уже обработанных таблиц, чтобы четко видеть, какие таблицы лежат за его пределами. Отношения оставшихся таблиц с облаком четко указывают - присоединяются ли они к нему сверху или снизу, или даже вообще не присоединяются напрямую, потому что перед этим необходимо обработать присоединение других таблиц. Позже в этой главе я подробнее рассмотрю этот вопрос.

Простые примеры

Ничто не иллюстрирует метод лучще, чем примеры, поэтому я приведу пример, используя диаграммы запроса, построенные в главе 5, начиная с простейшего случая, двустороннего соединения, показанного на рис. 6.1.

ЕОЛ 20

tO.98

d0.5

Рис. 6.1. Простое двустороннее соединение

Применяя первый шаг метода, сначала спросим себя, какой узел предлагает наилучший (наименьший) эффективный коэффициент фильтрации. Это будет узел Е, так как коэффициент фильтрации для Е, равный 0,1, меньще коэффициента D,

равного 0,5. Начиная с этого узла, выполним шаг 2 и обнаружим, что наилучшим (и единственным) узлом внизу будет узел D, поэтому перейдем к нему. Больше таблиц нет - следовательно, мы получили полный порядок соединения. Выполняя правила для надежного плана выполнения, к Е мы будет обращаться при помощи индекса по его фильтру, Exeript Fl ад. Затем по вложенным циклам через индекс по первичному ключу Departrient ID для Departments мы перейдем к соответствующим отделам. Применив грубую силу, в главе 5 я уже продемонстрировал, что этот план является наилучшим - по крайней мере, в терминах минимизации количества полученных строк.

ПРИМЕЧАНИЕ -

Правила для надежных планов и оптималышх надежных планов не учитывают, какие индексы у вас уже есть. Помните, что в этой главе рассматривается вопрос о том, какой план вам нужен, и этот вопрос не должен быть ограничен отсутствием необходимых индексов. Позже я рассмотрю случаи, когда можно довольствоваться неоптимальными планами, если какие-то индексы отсутствуют. Но вы должны сначала найти идеальные планы, а затем оценивать ситуацию и решать, идти ли на компромисс.

Порядок 8-стороннего соединения

Пока что все идет неплохо, но двусторонние соединения слишком просты, чтобы изучать новый метод, поэтому перейдем к следующему примеру, 8-стороннему соединению. Теоретически для восьми таблиц можно придумать 8! порядков соединения (то есть 40 320 вариантов) - достаточно для того, чтобы воспользоваться систематическим методом. Рисунок 6.2 повторяет задачу из главы 5.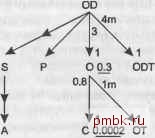

Рис. 6.2. Типичное 8-стороннее соединение

Воспользовавшись эвристическим методом, оптимальный порядок соединения для запроса, изображенного на диаграмме на рис. 6.2, можно определить следующим образом.

1. Найдем таблицу с наименьшим коэффициентом фильтрации. В этом случае это С с коэффициентом 0,0002, поэтому С становится ведущей таблицей.

2. Из С невозможно перейти вниз к какой-либо таблице через индекс по первичному ключу. Поэтому следует перейти по диаграмме вверх.

3. Единственный путь из С ведет к О, поэтому таблица О присоединяется второй.

4. После обработки О мы обнаруживаем, что теперь можно перейти вниз к ОТ. Когда возможно, всегда выбирайте путь вниз, и переходите вверх, только в случае, когда путей вниз не осталось. Таблица ОТ присоединяется третьей.

5. Ниже ОТ нет никаких таблиц, поэтому мы возвращаемся к О и переходим вверх к таблице 0D, которая присоединяется четвертой.

6. Все оставшиеся соединения ведут вниз и не фильтруются, поэтому соединения с S, Р и ODT можно выполнять в любом порядке.

7. Соединение с А можно выполнить в любой момент, но только после соединения с S, которое открывает путь к таблице А.

ПРИМЕЧАНИЕ

Я покажу, что при рассмотрении коэффициентов соединения вы всегда будете помещать ведущие вниз внутренние соединения перед внешними. Это происходит потому, что у внутренних соединений есть, по крайней мере, возможность отбрасывать строки, даже в таких случаях, как этот, когда статистика показывает, что соединение никак не повлияет на текущее количество строк.

Таким образом, мы обнаружили, что оптимальный порядок соединения можно описать как С; 0; ОТ; 0D; S, Р и ODT в любом порядке, а также А в любой момент после S. То есть допустимыми являются 12 одинаково хороших порядков соединения из 40 320 возможных. Изматывающий поиск всех возможных порядков соединения подтверждает, что эти 12 одинаково хороши. Их лучше всего использовать для минимизации количества полученных строк в надежных планах выполнения.

Диаграмма запроса может показаться вам слишком простой, чтобы представлять реальную проблему, но я обнаружил, что это совсем не так. В большинстве запросов даже с большим количеством соединений всего лишь один или два фильтра и один из коэффициентов фильтрации обычно очевидно лучше, чем остальные.

В большинстве случаев переход к наилучшему фильтру, за которым следуют соединения вниз, а затем соединения вверх и, возможно, обработка одного или двух незначительных фильтров по пути (лучше раньше, чем позже) - это все, что нужно для поиска отличного плана вьшолнения. Этот план практически всегда является наилучшим или так близок к наилучшему, что различия не играют большой роли. В этом случае мы получаем упрощенные диаграммы запросов. Полностью упрощенная диаграмма запроса, показанная на рис. 6.3, где наилучший фильтр обозначен заглавной буквой F, а второй - строчной буквой f, позволяет получить тот же результат, имея лишь качественную информацию о фильтре.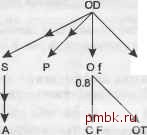

Рис. 6.3. Полностью упрощенная диаграмма запроса для того же 8-стороннего соединения

Я вернусь к этому примеру позже и покажу, что этот результат можно немного улучшить, ослабив требования для полностью надежного плана вьшолнения и ис-