полученных на первом, втором и третьем шагах вычисления. Новые кортежи получить невозможно, поэтому вычисление закончено и на рис. 4.23 изображено все отношение Connects. □

Рис. 4.23. Отношение Connects после третьего шага вычисления

4.4.4 Отрицание в рекурсивных правилах

Иногда в правилах, содержащих рекурсию, необходимо использовать отрицание. Есть опасный и безопасный способ соединения рекурсии с отрицанием. В общем случае считается приемлемым применять отрицание только тогда, когда оно не возникает внутри операции с фиксированной точкой. Рассмотрев приемлемый и парадоксальный примеры соединения рекурсии с отрицанием, мы увидим, что при наличии рекурсии полезно только стратифицированное отрицание. Определение термина стратифицированное дается после примеров.

Пример 4.39. Предположим, что нужно найти на схеме рис. 4.19 такие пары городов (х, у), чтобы самолет авиакомпании UA летел бы изхъ у (возможно, через несколько других городов), а самолет авиакомпании АА нет. Можно рекурсивно определить предикат UAreaches так же, как определялся предикат Reaches в примере 4.37, но ограничиться при этом рейсами UA:

1. UAreaches(x, у)

2. UAreaches(x, у)

- Flighfs(UA. х. у d. г)

- UAreaches(x, z) AND UAreaches(z. у)

Аналогично можно определить предикат AAreaches как такие пары городов (-v,j), что из л- можно попасть в .i- только самолетами А,А:

1. AAreaches(x, у) < - Frights(AA. х. у. О, г)

2. AAreacliesix. у) < - AAreaches(x. z) AND AAreaches(z. у)

Теперь с ПОМОШЬЮ нсрекчрсивного правила легко вычнсл1ггь предикат UAonly. состо-ЯШ1И1 из таких пар городов (.v.j-)- что из .v можно попасть в j-только рейсами UA, но не рейсами АА:

UAonly(x. у) <- UAreaches(x, у) AND NOT AAreaches(x, у)

По этому правилу вычисляется теоретико-множественная разность между UAreaches и AAreaches.

В соответствии с данными, представленными на рис. 4.19. UAreaches состоит нз пар: (SF, DEN), (SF, DAL), (SF, CHI), (SF, NY), (DEN, DAL). (DEN. CHI). (DEN, NY) и (CHI, NY). Это множество пар вычисляется итерированием операиии фиксированной точки, описанной в разделе 4.4.2. Ана-логнчно получается нз этих же данных и значение предиката AAreaches; (SF, DAL). (SF, CHI). (SF. NY), (DAL, CHI), (DAL, NY) H (CHI, NY). Значением предиката UAonly является разность между четырьмя этими множествами пар, т.е. (SF, DEN), (DEN, DAL), (DEN, CHI) и (DEN, NY). □

Пример 4.40. Приведем абстрактный пример, который будет посложнее прсды-луших. Пусть Л-единственный унарный (одноместны!*) предикат EDB с единственным кортежем (0), а / и С- одноместные унарные предикаты IDB, определяемые двумя правилами:

1. P(x)<-R(x) AND NOT Q(x)

2. Q(x) <- R(x) AND NOT P(x)

Неформально говоря, эти правила означают, что элемент А из Л входит либо в Р, либо в Q. При этом Ри Q определяются рекурсивно в терминах друг друга.

При выяснении смысла рекурсивных правил в разделе 4.4.1 говорилось, что нужна наименьшая фиксированная точка - наименьшие отношения, делающие данные правила истинными алгебраическими выражениями. Согласно правилу I, Р = R - Q. а по правилу 2, R~P. Поскольку R содержит только кортеж (0), он находится либо в Р. либо в Q. Где же именно находится данный кортеж? Оказывается, он не может входить нн в Р. нн в Q. Например, из Р= R- Q следует 0 = {Ф)) - 0. что явно ложно.

Если Р={(0)}. а 0=0. оба уравнения имеют решения. Р= R-QjxRtT {(0)1 = ((O)j 0, что истинно, и Q= R- Р дает 0= {(0)1 - {(0)), что тоже истинно.

Значения Р = 0 и О =((0)1 тоже удовлетворяют обоим правилам. Значит, есть два варианта значений:

a) Р =1(0)1 0=0

b) /=0. G-I(O)}

Онн оба минимальны п том смысле, что при удалении любого кортежа из любого отношении, рассматриваемые отношения уже не удовлетворяют правилам. Следовательно, невозможно различить две минимальные фиксированные точки (а) и (Ь) и ответить на простой вопрос: я1У1яется ли Р(0) истинным? □

UAonly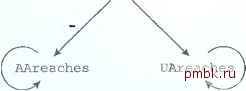

Рис. 4.24. Граф, ПОСТРОЕННЫЙ по стротифицировонной рекурсии

Данный пример показывает, что метод определения смысла рекурсивных правил или уравнений с фиксированной точкой не действует, когда рекурсия слишком тесно связана с отрицанием. Допустим, существует несколько минимальных фиксированных точек, между когорыми может возникнуть противоречие. Было бы желательно иметь более эффективный метод определения смысла рекурсивного отрицания, ио, к сожалению, общего соглашения о том. что должны означать такие правила или уравнения, нет.

Поэтому принято ограничиваться рекурсиями со стратифицированным (расслоенным) отрицанием. Такое ограничение вводится, например, стандартом рекурсии SQL3, о котором пойдет речь в разделе 5.10. Позже будет показано, что при стратифицированном отрицании существует алгоритм вычисления определенной минимальной фиксированной точки (возможно, из множества фиксированных точек), соответствующий интуитивному пониманию смысла правил. Свойство стратифицированиости определяется следующим образом.

1. Строится граф, состветствующий предикатам 1DB.

2. Если в правило, содержащее предикат j4 в своей голове, входит отрицательная подцель В, от узла А к узлу В проводится ориентированное ребро, которое помечается знаком - как отрицателы{ое ребро.

3. Если в правило, содержащее предикат А в своей голове, входит несугрица-тельная подцель В, от узла А к узлу В проводится обычное ориентированное ребро, не отмеченное знаком отрицания

Если в этом графе есть цикл, содержащий одно или несколько отрицательных ребер, рекурсия не стратифицирована, в противном случае граф стратифицирован. Предикаты 1DB можно сгруппировать в слои. Слой предиката А -это наибольшее число отрицательных ребер на прти, начинающемся с А.

При стратифицированной рекурсии предикаты ЮВ можно оценивать в порядке их слоев, начиная с первого. Такая стратегия дает одну из минимальных фиксированных точек используемых правил. Еще важнее то, что она всегда оказывается эффективной и позволяет получить правильную фиксированную точку. А нестра-тифицированная рекурсия, как показывает пример 4.40, может вообще не привести ни к какой правильной фиксированной точке, даже если есть широкий выбор фиксированных точек.

Пример 4.41. На рис. 4.24 изображен граф для предикатов из примера 4.39. AAreaches и UAreaches находятся в слое О, так как ни один из путей, начинающихся в их узлах, не содержит негативного ребра. UAonly относится к слою t, потому что из этого узла выходят пути с одним негативным ребром, но нет путей, содержащих более одного негативного ребра. Значит, прежде чем вычислять UAonly, нужно полностью вычислить AAreaches и UAreaches,