Правила примера 4.36 - это абсолютно то же самое, что уравнения с фиксированной точкой из примера 4.35, поэтому вычисление значения FollowOn для эти.к правил идентично вычислению из примера 4.35. В обшем случае при вычислении значений отношений 1DB, определяемых множеством правил Daialog без отрицательных подцелей, можно начинать с пустого множества отношений IDB и итеративно вычислять новые значения отношений IDB. применяя правила к отношениям EDB и к предыдущим значениям до тех пор, пока отношения IDB не перестанут изменяться

Пример 4.37. Более сложные примеры применения рекурсии можно найти при анализе п\тей в графах. На рис. 4.19 показан граф, представляющий рейсы двух гипотетических авиалиний - Unmed Airlines (UA) и Arcane .Airlines (АЛ) - между городами Сан-Франциско, Денвер, Даллас, Чикаго и Нью-Йорк.

1500-1800

930-1230

АА 1900-2200 UA1830-2130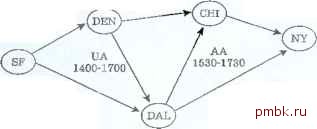

АА 900-1430

АА 1500-1930

Рис. 4.19. Порто ааиорейсое

Авиарейсы можно представить отношением EDB:

Flights(ajriine, from, to, departs, arrives) Кортежи этого отношения для данных из рис. 4.19 показаны на рис. 4.20.

Рис. 4.20. Кортежи отношений Flights

5 Эти правила работают только гри допущении, что самолеты не вычетают и не прилетают точно в полночь.

Самый простой рекурсивный запрос; указЕп-ь такие пары городов, чтобы из города X можно было попасть а город у одним авнарейсом или более. Отношение Reaches(x, у), содержащее именно такие пары городов, описывается двумя правилами:

1. Reaches(x, у) -(- FlightE(a, х, у, d, г)

2. Reaches{x, у) <- Reaches(x, z) AND Reaches(z, у)

Согласно первому правилу, Reaches содержит такие пары городов, что из первого из них можно попасть прямым авиарейсом. В этом правиле рейс а, время вылета d и время прилета г произвольны. Согласно второму правилу, если из города X можно попасть в город г, а из г в у, то из х можно попасть в у. Здесь применяется нелинейная рекурсия, которая описывается в выделенном тексте, озаглавленном Другие формы рекурсии . Такая рекурсия в данном случае более уместна, так как второе применение Flights в рекурсивном правиле содержит еще три переменные для неиспользованных компонентов Flights.

Вычисление отношения Reaches проводится с помощью рекурсивного процесса, описанного в разделе 4.4.2. С помощью первого правила получаются пары (SF, DEN). (SF, ОАЦ, (DEN, СНГ), (DAL, СНГ), (DAL, NY) и (CHI, NY). представленные ориентированными ребрами графа на рис. 4.19.

Затем по второму рек)рсивному правилу получаются еще три пары; (CF, CHI), (DEN, NY) и (SF, NY). На следующем шаге эти пары, представленные двумя ребрами, комбинируются с парами, каждая из которых представлена только одним ориентированным ребром, и получаются пути в графе длиной до четырех ориентированных ребер. Для данной диаграммы уже невозможно сформировать новую пару. Значит, отношение Reacties состоит из десяти таких пар [х,у), что на рис. 4.19 у находится справа от х. □

Пример 4.38. Еще более сложное определение, в котором два авиарейса можно комбинировать в более длинные последовательности, состоит в требовании, чтобы самолет второго рейса покидал аэропорт не раньше чем через час после прибытия в этот аэропорт самолета первого рейса. При этом применяется ЮВ-предикат Connects(x, у, d, г), означающий, что можно вылететь из города х во время d и несколькими рейсами добраться до города у во время г. Если между рейсами имеется связь, то есть по крайней мере не меньше часа на то, чтобы ее использовать. Правила лля Connect:

1. Connectsfx, у, d, г) FIights(a, х, у, d, г)

2. Connects(x, у, d, г) Connects(x, z. d, tl) AND

Connects(z, y, 12, r) AND tl <= 12+100

Ha первом шаге вычисления правило 1 дает восемь кортежей отношения Connects, показанных на рис. 4.21, каждый из которых соответствует одному из авиарейсов, представленных на диаграмме рис. 4.19. Заметим, что одно из семи ориентированных ребер этой диаграммы представляет два рейса в различное время.

Теперь попытаемся комбинировать эти кортежи по правилу 2. Например, соединение второго кортежа с пятым дает (CF, CHI, 900, 1730), но второй кортеж не комбинируется с шестым, так как самолет прибывает в Даллас в 14.30, а вылетает из Далласа в 15.00, т.е. через полчаса. На рис. 4.22 показаны кортежи Connects, полученные после второго шага. Результат второго шага отделен от результата первого горизонтальной чертой, которая не является частью отношения.

Рис. 4.21. бозовые кортежи отношения Connects

Иа третьем шаге все пары кортежей, показанных на рис. 4.22, нужно рассматривать, в принципе, в качестве кашидатов для двух кортежей Connects, входяших в тело правила 2. Однако, если оба кортежа находятся над горизонтальной линией, значит, они уже анализировались на предыдущем шаге и не могут породить нового кортежа. Получить новый кортеж можно только тогда, когда по крайней мере один из двух кортежей отношения Connects, используемого в теле правила 2, был получен на втором uiare; т.е. нужно использовать кортежи, находящиеся на рис. 4.42 под горизонтальной линией.

Рис. 4.22. Отношение Connects после iaroporo цюго вычисления

На третьем шаге получаются три новых кортежа, находящихся в нижней части pig3. Дщизонщщ,1е Л1Щ1нуто1аблииы разделяют группы кортежей.