Упрожнение 3.4.2. На рис. 3.24 дано ODL-описание схемы, аналогичной E/R-диаграмме из упражнения 3.4.1. Конвертируйте его в схему реляционной БД. Помните, что объекты Course могут быть однозначно идентифицированы и допускается ввести атрибут, представляющий это свойство, например CourselD. В этом упражнении е рс/со/гелср/пся имитировать стратегию, в упражнении 3.4.1 применяемую для конвертирования слабого множества сущностей (хотя, в принципе, это можно сделать).

interface Course { attribute int number; attribute string room;

relationsirip Dept deptOf inverse Dept::coursesOf;

interface LabCoorse: Course { attribute int computerAlloc;

interface Dept {

unique attribute string name; attribute string cliair; relationship Set<Course> coursesOf inverse Course::deptOf;

Рис. 3.24. ODl-ontKQHMe теоретически! и лоборотсзрных курсов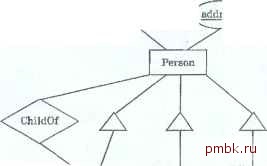

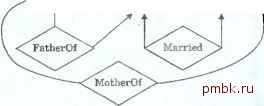Рис. 3.25. б/В-диофоммо к упрожненио 3.4.5

Упражнение З.в.З. К.онвертируПте в схемы реляционных БД ODL-проекты; *л) 43 упражнения 2.4.1: Ь) из упразднения 2.4 4.

Упражнение 3.4.4. Конвертируйте в схемы реляционных БД E/R-проекты; *а) из упра;?у1сния 2.4.3: Ь) из упражнения 2.4.4.

! Упрожнение 3.4.5. Конвертируйте показанную на рнс. 3.25 E/R-диаграмму в схему реляционно i БД.

! Нпрожнение 3.4.6. Как будет выглядеть скеш реляционной БД из упражнения 3.4.5, если начать ее !юстрое11ие с соответствующего определения ODL?

3.5 Функциональные зависимости

Самый важный вид ограничений, применяемых в реляционной модели, ограничение по уникальности значений, называемое функциональной зависимостью. Знать такое о раниче ие просто необходимо для того, чтобы перерабатывать схемы БД с целью устранения избыточности (см. раздел 3.7). Существуют и другие ограничения, позволяющие создавать хорошие схемы БД: многозначные зависимости (см. раздел 3.8), ограниченгы существования и ограничения независимости (см. раздел 4.5).

3.5.1 Определение

функциональной зависимости

Функциональная зависимость на отношении Л -это утверждение вида Если два кортежа R совпадают по атрибутам А А, ..,А (т.е. эти кортежи имеют в соответствующих друг другу компонентах одни и тс же значения для каждого из перечисленных атрибутов), то они должны совпадать и по другому атрибуту Я. Формально эта зависимость записывается выражением А,А2 - А ->В, причем говорится, что Ai. А}.....А функционально определяю! В.

As

В s

Если t iiu совпадают здесь

Тогда t и u совпадают и здесь

Рис. 5.26. Эффект функциональной зовгкииости но двух кортежсвс

Если множество атрибугов А,.А2,...,А одного атрибута, иапри.мер.

функционально определяют более

/), А2... А

А,А ...A - Д

то даттое множество зависимостей можно записать сокращенно: А,А,...А - В,

На рис. 3.26 показана функциональная зависимость между любыми двумя кортежами /ИИ отношения R.

Пример 3.20. Рассмотрим отношение Movie из рис. 3.13, экземпляр которого воспроизведен на рис. 3.27.

Рие. 3.27. Отношение Movie

в этом отношении можно установить множество функциональных зависимостей, например:

title year -* length title year filmType title year studioName

Поскольку левые части этих лависимостей совпадают, их можно записать одной строкой:

title year -> length filmType studioName

Неформально это множество зависимостей означает: если два кортежа имеют одно и то же значение в своих компонентах title и одно и то же значение в компонентах year, то они должны иметь одинаковые значения в компонентах length, одинаковые значения в компонентах filmType и одинаковые значения в компонентах StudioName. Такое утверждение имеет смысл, если вспомнить исходный проект, из которого была построена реляционная схема Movie. Атрибуты title и year образуют ключ для объектов из множества фильмов. Поэтому при наличии названия и гола выпуска фильма, существуют также его уникальная длина, уникальный тип и единственная владеющая им студия.

В то же время утверждение

title year -> starName